寒假学习计划
比赛地址
[A] 牛牛的DRB迷宫I
题意
给出一个迷宫,每个格子有一个字母,标志着站在这个格子上的时候能向右,向下,还是向右或向下走.一个人初始站在左上角,求走到右下角有多少种方案.
题解
签到题
代码
#include<cstring>
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<vector>
#include<cmath>
#define l(x) (x<<1)
#define r(x) ((x<<1)+1)
#define LL long long
#define N 55
#define MOD 1000000007
#define INF 0x3f3f3f3f
using namespace std;
int n,m,i,j;
int a[N][N];
char c[N][N];
LL f[N][N];
inline int Abs(int x){return (x<0)?-x:x;}
inline void Swap(int &a,int &b){a^=b^=a^=b;}
inline int Min(int a,int b){return (a<b)?a:b;}
inline int Max(int a,int b){return (a>b)?a:b;}
inline int read(){
int p=0,f=1; char c=getchar();
while (c<48||c>57) {if (c=='-') f=-1; c=getchar();}
while (c>=48&&c<=57) p=(p<<1)+(p<<3)+c-48,c=getchar();
return p*f;
}
inline void Ready(){
int i=0,j=0;
for (i=1;i<=n;i++)
for (j=0;j<m;j++)
if (c[i][j]=='R') a[i][j+1]=1;
else if (c[i][j]=='D') a[i][j+1]=2;
else a[i][j+1]=3;
}
int main(){
#ifdef __Marvolo
freopen("zht.in","r",stdin);
freopen("zht.out","w",stdout);
#endif
scanf("%d%d",&n,&m);
for (i=1;i<=n;i++)
scanf("%s",&c[i]);
Ready();
memset(f,0,sizeof(f));
f[1][1]=1;
for (i=1;i<=n;i++)
for (j=1;j<=m;j++){
if (a[i][j]==1) f[i][j+1]=(f[i][j+1]+f[i][j])%MOD;
else if (a[i][j]==2) f[i+1][j]=(f[i+1][j]+f[i][j])%MOD;
else {
f[i][j+1]=(f[i][j+1]+f[i][j])%MOD;
f[i+1][j]=(f[i+1][j]+f[i][j])%MOD;
}
}
cout<<f[n][m]%MOD<<endl;
return 0;
}
[B] 牛牛的DRB迷宫II
题意
和第一题基本一样.不过是反过来,给出方案数让你构造一个迷宫.
题解
很有意思的一个构造.
思路如下图:
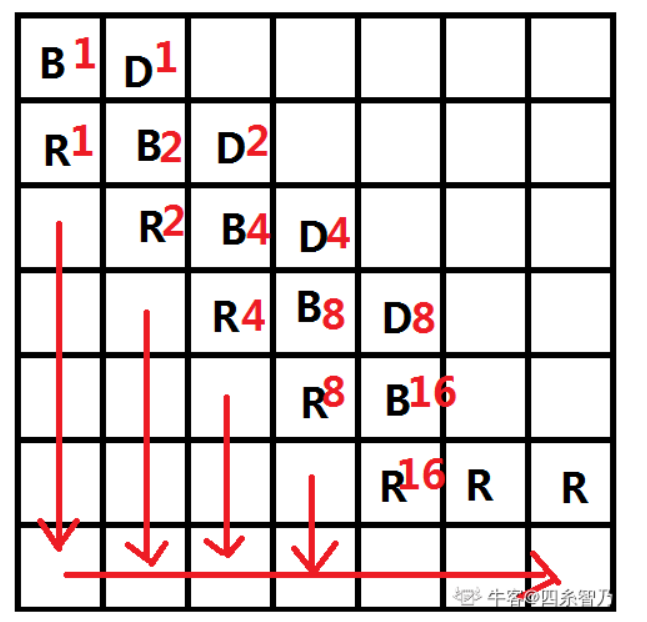
之后按照二进制拆分就好了.
代码
#include<cstring>
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<vector>
#include<cmath>
#define l(x) (x<<1)
#define r(x) ((x<<1)+1)
#define LL long long
#define N 55
#define INF 0x3f3f3f3f
using namespace std;
int i,j,k;
char c[N][N];
inline int Abs(int x){return (x<0)?-x:x;}
inline void Swap(int &a,int &b){a^=b^=a^=b;}
inline int Min(int a,int b){return (a<b)?a:b;}
inline int Max(int a,int b){return (a>b)?a:b;}
inline int read(){
int p=0,f=1; char c=getchar();
while (c<48||c>57) {if (c=='-') f=-1; c=getchar();}
while (c>=48&&c<=57) p=(p<<1)+(p<<3)+c-48,c=getchar();
return p*f;
}
int main(){
#ifdef __Marvolo
freopen("zht.in","r",stdin);
freopen("zht.out","w",stdout);
#endif
scanf("%d",&k);
printf("50 50\n");
for (i=0;i<50;i++)
for (j=0;j<50;j++)
c[i][j]='R';
for (i=0;i<=30;i++) c[i][i]='B';
for (i=0;i<30;i++) c[i][i+1]='D';
for (i=0;i<=30;i++){
if (k&(1<<i)){
for (j=i+1;j<=50;j++)
c[j][i]='D';
c[i+1][i]='B';
}
}
for (i=0;i<50;i++)
c[49][i]='R';
for (i=0;i<50;i++){
for (j=0;j<50;j++)
putchar(c[i][j]);
putchar(10);
}
return 0;
}
[C] 牛牛的数组越位
题意
有一个二维数组和一些赋值操作,给出数组溢出时的规律,判断这些操作中是否存在非法操作,是否存在导致越界的非法操作.
题解
签到题
代码
#include<cstring>
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<vector>
#include<cmath>
#define l(x) (x<<1)
#define r(x) ((x<<1)+1)
#define LL long long
#define N 1010
#define INF 0x3f3f3f3f
using namespace std;
int T,i,j,x,y,n,m,tag,flag,val,w,p;
int a[N][N],b[N][N];
inline int Abs(int x){return (x<0)?-x:x;}
inline void Swap(int &a,int &b){a^=b^=a^=b;}
inline int Min(int a,int b){return (a<b)?a:b;}
inline int Max(int a,int b){return (a>b)?a:b;}
inline int read(){
int p=0,f=1; char c=getchar();
while (c<48||c>57) {if (c=='-') f=-1; c=getchar();}
while (c>=48&&c<=57) p=(p<<1)+(p<<3)+c-48,c=getchar();
return p*f;
}
int main(){
#ifdef __Marvolo
freopen("zht.in","r",stdin);
freopen("zht.out","w",stdout);
#endif
T=read();
while (T--){
n=read(); m=read(); p=read();
flag=0; tag++;
while (p--){
x=read(); y=read(); val=read();
w=x*m+y;
if (w > m*n-1 || w<0){
flag=2;
continue;
}
if (x<0 || y<0 || x>n-1 || y>m-1){
if (flag==0) flag=1;
a[w/m][w%m]=val;
b[w/m][w%m]=tag;
continue;
}
a[x][y]=val; b[x][y]=tag;
}
if (flag==2){
puts("Runtime error");
continue;
}
for (i=0;i<n;i++){
for (j=0;j<m-1;j++)
if (b[i][j]==tag) printf("%d ",a[i][j]);
else printf("0 ");
if (b[i][m-1]==tag) printf("%d\n",a[i][m-1]);
else printf("0\n");
}
if (flag==0) puts("Accepted");
else if (flag==1) puts("Undefined Behaviour");
}
return 0;
}
[D] 牛牛与二叉树的数组存储
题意
给出一个长度为n的数组,表示一棵二叉树.第一位为根节点编号,第i位的左儿子在2i位,右儿子在2i+1位.不存在则为-1.要求把这棵二叉树每个节点的信息输出出来.
题解
签到题
代码
#include<cstring>
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<vector>
#include<cmath>
#define l(x) (x<<1)
#define r(x) ((x<<1)+1)
#define LL long long
#define N 500010
#define INF 0x3f3f3f3f
using namespace std;
int n,i,tot;
int a[N],f[N],l[N],r[N];
inline int Abs(int x){return (x<0)?-x:x;}
inline void Swap(int &a,int &b){a^=b^=a^=b;}
inline int Min(int a,int b){return (a<b)?a:b;}
inline int Max(int a,int b){return (a>b)?a:b;}
inline int read(){
int p=0,f=1; char c=getchar();
while (c<48||c>57) {if (c=='-') f=-1; c=getchar();}
while (c>=48&&c<=57) p=(p<<1)+(p<<3)+c-48,c=getchar();
return p*f;
}
inline void Dfs(int x,int id){
if (id == -1) return;
if (a[2*x]>0) l[id]=a[2*x],f[a[2*x]]=id,Dfs(2*x,a[2*x]);
if (a[2*x+1]>0) r[id]=a[2*x+1],f[a[2*x+1]]=id,Dfs(2*x+1,a[2*x+1]);
}
int main(){
#ifdef __Marvolo
freopen("zht.in","r",stdin);
freopen("zht.out","w",stdout);
#endif
scanf("%d",&n);
for (i=1;i<=n;i++) a[i]=read();
for (i=1;i<=n;i++)
if (a[i]>0) tot++;
printf("The size of the tree is %d\n",tot);
printf("Node %d is the root node of the tree\n",a[1]);
for (i=1;i<=tot;i++)
f[i]=l[i]=r[i]=-1;
Dfs(1,a[1]);
for (i=1;i<=tot;i++)
printf("The father of node %d is %d, the left child is %d, and the right child is %d\n",i,f[i],l[i],r[i]);
return 0;
}
[E] 牛牛的随机数
题意
给出l_1,r_1,l_2,r_2.现在从[l_1,r_1]和[l_2,r_2]各选择一个数,求两数异或的期望值.
题解
显然是按位考虑.假设两个区间长度分别为L_1,L_2.第一个区间二进制第i位不为0的数有a个,第二个区间有b个.则对答案的贡献是2^{i}[a(L_2-b)+b(L_1-a)]
问题转化为了a与b的计算.使用数位DP即可.
下面的代码是WA的,由于莫名的原因最后一个点一直过不去,有空了再回来Debug一下.
代码
#pragma GCC optimize(3)
#include<cstring>
#include<cstdio>
#include<iostream>
#define LL long long
using namespace std;
LL T,l1,l2,r1,r2,Ans,l,L,inv,inv2,i,s,p,q,t;
int len,flag;
int z[62];
LL f[62][60];
const LL MOD=1000000007;
namespace IO {
const int MAXSIZE =1<<20;
char buf[MAXSIZE],*p1,*p2;
#define gc()(p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, MAXSIZE, stdin), p1 == p2)?EOF:*p1++)
inline LL rd() {
register LL x=0,f=1;
char c = gc();
while (!isdigit(c)){
if (c=='-') f=-1;
c=gc();
}
while (isdigit(c)) x=(x<<3)+(x<<1)+(c^48),c=gc();
return x*f;
}
};
using namespace IO;
inline LL Mi(LL x,LL y){
LL p=x,t=1,Res=1;
for (;t<=y;(t&y)?Res=(Res*p)%MOD:0,p=(p*p)%MOD,t<<=1);
return Res;
}
inline LL Dfs(int pos,int cnt,int limit){
register LL i=0,up=0,sum=0;
if (pos>len) return cnt;
if (!limit && f[pos][cnt]!=-1) return f[pos][cnt];
up=(limit)?z[len-pos+1]:1;
for (i=0;i<=up;i++)
sum+=Dfs(pos+1,cnt+(i && (len-pos)==flag),limit&&(i==up));
return (!limit)?f[pos][cnt]=sum:sum;
}
inline LL Cal(LL r,LL x){
len=0; memset(f,-1,sizeof(f));
if (!r) return 0;
while (r){z[++len]=r%2; r>>=1;}
flag=x;
return (len<x+1)?0:Dfs(1,0,1)%MOD;
}
int main(){
#ifdef __Marvolo
freopen("zht.in","r",stdin);
freopen("zht.out","w",stdout);
#endif
T=rd();
while (T--){
l1=rd(); r1=rd(); l2=rd(); r2=rd();
if (l1==r1 && l2==r2){
Ans=(l1&l2)%MOD;
printf("%lld\n",Ans);
continue;
}
l=(r1-l1+1)%MOD; L=(r2-l2+1)%MOD;
inv=Mi(l,MOD-2); inv2=Mi(L,MOD-2);
inv=(inv*inv2)%MOD; Ans=0; t=1;
for (i=0;i<=60;i++){
if (t>r1 && t>r2) break;
p=(t>r1)?0:(Cal(r1,i)-Cal(l1-1,i)+MOD)%MOD;
q=(t>r2)?0:(Cal(r2,i)-Cal(l2-1,i)+MOD)%MOD;
s=(p*((L-q+MOD)%MOD)%MOD+q*((l-p+MOD)%MOD)%MOD)%MOD;
s=(s*(t%MOD))%MOD; Ans=(Ans+s)%MOD;
t<<=1;
}
while (Ans<0) Ans+=MOD;
Ans=(Ans*inv)%MOD;
printf("%lld\n",Ans);
}
return 0;
}
[F] 牛牛的Link Power I
题意
给出一个长度为n的数组,第i位要么为0,要么为1.如果第i位为1,则称其处于Link状态.定义Link Power为
\sum_{a_{i}=a_{j}=1}Abs(i-j)
求这个数组的Link Power值.
题解
从前向后计算.
假设算到了第i位,前面有k个数处于Link状态,其下标之和为sum.不难算出其对答案的贡献是ki-sum.不断更新k和sum即可.
代码
#include<cstring>
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<vector>
#include<cmath>
#define l(x) (x<<1)
#define r(x) ((x<<1)+1)
#define LL long long
#define N 100010
#define MOD 1000000007
#define INF 0x3f3f3f3f
using namespace std;
int n,i;
LL Ans,l,sum;
int a[N];
char c[N];
vector <LL> v;
inline int Abs(int x){return (x<0)?-x:x;}
inline void Swap(int &a,int &b){a^=b^=a^=b;}
inline int Min(int a,int b){return (a<b)?a:b;}
inline int Max(int a,int b){return (a>b)?a:b;}
inline int read(){
int p=0,f=1; char c=getchar();
while (c<48||c>57) {if (c=='-') f=-1; c=getchar();}
while (c>=48&&c<=57) p=(p<<1)+(p<<3)+c-48,c=getchar();
return p*f;
}
int main(){
#ifdef __Marvolo
freopen("zht.in","r",stdin);
freopen("zht.out","w",stdout);
#endif
n=read();
scanf("%s",&c);
for (i=0;i<n;i++) a[i+1]=c[i]-48;
for (i=1;i<=n;i++)
if (a[i]==1) v.push_back(i);
Ans=l=sum=0;
for (auto j : v){
if (!l){
l=j; sum++; continue;
}
Ans=(Ans+((sum*j)%MOD-l+MOD)%MOD)%MOD;
l=(l+j)%MOD; sum++;
}
cout<<Ans%MOD<<endl;
return 0;
}
[G] 牛牛的Link Power II
题意
同上题.不过这次多了一个修改操作,每一次操作会把某一位异或上1.求每次操作后的Link Power值.
题解
类似的计算思路,用树状数组维护上面提到的k和sum.每一次操作计算变化量即可.
代码
#include<cstring>
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<vector>
#include<cmath>
#define l(x) (x<<1)
#define r(x) ((x<<1)+1)
#define bit(x) (x&(-x))
#define LL long long
#define N 400010
#define MOD 1000000007
#define INF 0x3f3f3f3f
using namespace std;
int n,i,m;
LL Ans,s,cnt,x,y;
int a[N];
char C[N];
vector <LL> v;
struct Tree{
LL b[N];
inline void Ready(){memset(b,0,sizeof(b));}
inline LL Que(LL x){
LL An=0,i=0;
if (!x) return 0;
for (i=x;i;i-=bit(i)) An=(An+b[i]+MOD)%MOD;
return An;
}
inline LL Query(LL l,LL r){
if (l>r) return 0;
if (!r || l>n) return 0;
return (Que(r)-Que(l-1)+MOD)%MOD;
}
inline void Add(LL x,LL val){
LL i=0;
for (i=x;i<=n;i+=bit(i)) b[i]=(b[i]+val+MOD)%MOD;
}
}A,B;
inline void Ready(){
LL l=0,sum=0;
for (i=1;i<=n;i++)
if (a[i]==1){
v.push_back(i);
A.Add(i,i); B.Add(i,1);
}
Ans=l=sum=0;
for (auto j : v){
if (!l){
l=j; sum++; continue;
}
Ans=(Ans+((sum*j)%MOD-l+MOD)%MOD)%MOD;
l=(l+j)%MOD; sum++;
}
}
int main(){
#ifdef __Marvolo
freopen("zht.in","r",stdin);
freopen("zht.out","w",stdout);
#endif
scanf("%d",&n);
scanf("%s",C);
for (i=1;i<=n;i++) a[i]=C[i-1]-48;
A.Ready(); B.Ready();
Ready(); printf("%lld\n",Ans);
scanf("%d",&m);
while (m--){
scanf("%lld%lld",&x,&y);
if (x==1){
s=B.Query(1,y-1); cnt=A.Query(1,y-1);
Ans=(Ans+((s*y)%MOD)-cnt+MOD)%MOD;
s=B.Query(y+1,n); cnt=A.Query(y+1,n);
Ans=(Ans-((s*y)%MOD)+cnt+MOD)%MOD;
A.Add(y,y); B.Add(y,1);
printf("%lld\n",Ans%MOD);
} else {
s=B.Query(1,y-1); cnt=A.Query(1,y-1);
Ans=(Ans-((s*y)%MOD)+cnt+MOD)%MOD;
s=B.Query(y+1,n); cnt=A.Query(y+1,n);
Ans=(Ans+((s*y)%MOD)-cnt+MOD)%MOD;
A.Add(y,-y); B.Add(y,-1);
printf("%lld\n",Ans%MOD);
}
}
return 0;
}
[H] 牛牛的k合因子数
题意
若一个数的所有因子中恰有k个为合数,则称其为k合因子数.求1-n中有多少k合因子数.
题解
线性筛预处理,然后直接计算.
代码
#include<cstring>
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<vector>
#include<cmath>
#define l(x) (x<<1)
#define r(x) ((x<<1)+1)
#define LL long long
#define N 400010
#define NN 100000
#define INF 0x3f3f3f3f
using namespace std;
int n,m,i,x;
int ans[N],v[N],p[N];
inline int Abs(int x){return (x<0)?-x:x;}
inline void Swap(int &a,int &b){a^=b^=a^=b;}
inline int Min(int a,int b){return (a<b)?a:b;}
inline int Max(int a,int b){return (a>b)?a:b;}
inline int read(){
int p=0,f=1; char c=getchar();
while (c<48||c>57) {if (c=='-') f=-1; c=getchar();}
while (c>=48&&c<=57) p=(p<<1)+(p<<3)+c-48,c=getchar();
return p*f;
}
inline void Ready(){
LL i=0,j=0,x=0,sum=0;
v[1]=-1;
for (i=2;i<=n;i++){
if (v[i]) continue;
for (j=i*i;j<=n;j+=i) v[j]=1;
}
for (i=1;i<=n;i++){
x=int(sqrt(i)); sum=0;
for (j=1;j<=x;j++){
if (!(i%j)){
if (v[j]==1) sum++;
if ((j*j)!=i && v[i/j]==1) sum++;
}
}
ans[sum]++;
}
}
int main(){
#ifdef __Marvolo
freopen("zht.in","r",stdin);
freopen("zht.out","w",stdout);
#endif
n=read(); m=read();
memset(ans,0,sizeof(ans));
Ready();
while (m--){
x=read();
printf("%d\n",ans[x]);
}
return 0;
}
[I] 牛牛的汉诺塔
题意
给出一个含有n个圆盘的汉诺塔.三根柱子从左到右编号为A,B,C.所有的圆盘都在最左边的柱子上,要挪到最右边.求A->B,A-C,...,B-C这6种移动情况各发生了多少次,以及总共挪了多少次.
题解
显然总的次数为2^{n}-1
题解给的方法是记忆化,或者使用递推.笨办法是直接暴力找规律...
Python大法好
代码
n=int(input())
f=[0 for i in range(10)]
s=(n//2)-1
f[1]=f[4]=(3*s+1+2**(2*s+3))//9
s=((n+1)//2)-1
f[2]=(4**(s+1)+6*s+5)//9
s=(n-1)//2
f[3]=f[6]=(4**(s+1)-3*s-4)//9
s=(n-2)//2
f[5]=2*(4**(s+1)-3*s-4)//9
print("A->B:%d"%(f[1]))
print("A->C:%d"%(f[2]))
print("B->A:%d"%(f[3]))
print("B->C:%d"%(f[4]))
print("C->A:%d"%(f[5]))
print("C->B:%d"%(f[6]))
print("SUM:%d"%((2**(n))-1))
[J] 牛牛的宝可梦Go
题意
给出一个无向图,边权为1.现在有k个宝可梦会在一些时刻出现在某个点上.每个宝可梦有一个价值.玩家初始站在1号点,时刻为0.每个时刻前可以移动到相邻的点上.如果在移动完毕后,恰好有个宝可梦出现在移动到的点上,就可以把它捕捉,否则下一时刻宝可梦就会消失.求最多能获得多少价值.
题解
设dp[i]表示捕捉到第i只宝可梦所获得的最大价值.显然有转移方程:
dp[i]=Max(dp[i],dp[j]+val_i),dis[i][j]\leq t_{i}-t_{j}
但是朴素的转移是O(n^2)的,n=1e5.一般情况是不能接受的.所以需要一点优化.
因为图不大,只有200个点.而且题目保证一个时刻只会出现一个宝可梦,所以只需要枚举第i个宝可梦的前200个出现的宝可梦转移就行了.再之前的肯定能够移动过来(前提是连通),故只需再维护一个最大值即可.
代码
#include<cstring>
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<vector>
#include<cmath>
#define LL long long
#define N 200010
#define INF 0x3f3f3f3fll
using namespace std;
LL n,m,i,x,y,k;
LL dis[210][210];
LL dp[N],w[210];
struct Data{
LL x,y,val;
}a[N];
inline LL Min(LL a,LL b){return (a<b)?a:b;}
inline LL Max(LL a,LL b){return (a>b)?a:b;}
inline bool cmp(const Data &a,const Data &b){return a.x<b.x;}
inline LL read(){
LL p=0,f=1; char c=getchar();
while (c<48||c>57) {if (c=='-') f=-1; c=getchar();}
while (c>=48&&c<=57) p=(p<<1)+(p<<3)+c-48,c=getchar();
return p*f;
}
inline void Ready(){
register int i=0,j=0,k=0;
for (k=1;k<=n;++k)
for (i=1;i<=n;++i)
for (j=1;j<=n;++j)
dis[i][j]=Min(dis[i][j],dis[i][k]+dis[k][j]);
}
inline void Work(){
register int i=0,j=0;
LL Ans=0;
for (i=1;i<=n;i++) w[i]=-INF;
for (i=1;i<=k;i++){
dp[i]=-1e18;
if (dis[1][a[i].y] <= a[i].x)
dp[i]=a[i].val;
for (j=Max(1,i-n);j<i;j++){
if (dis[a[i].y][a[j].y] > a[i].x-a[j].x) continue;
dp[i]=Max(dp[i],dp[j]+a[i].val);
}
if (i>n){
for (j=1;j<=n;j++)
if (dis[a[i].y][j] < INF)
dp[i]=Max(w[j]+a[i].val,dp[i]);
w[a[i-n].y]=Max(w[a[i-n].y],dp[i-n]);
}
Ans=Max(Ans,dp[i]);
}
cout<<Ans<<endl;
}
int main(){
#ifdef __Marvolo
freopen("zht.in","r",stdin);
freopen("zht.out","w",stdout);
#endif
n=read(); m=read();
memset(dis,INF,sizeof(dis));
for (i=1;i<=m;i++){
x=read(); y=read();
dis[x][y]=dis[y][x]=1;
}
for (i=1;i<=n;i++) dis[i][i]=0;
Ready();
k=read();
for (i=1;i<=k;i++){
a[i].x=read(); a[i].y=read(); a[i].val=read();
}
sort(a+1,a+1+k,cmp);
Work();
return 0;
}
总结
寒假基础训练第五场.
感觉是这个系列比赛中质量最低的一场了.
出题人好像很偏爱浮点数,出了n多道浮点数计算相关的问题,卡常,卡一些做法,题目描述各种不清晰,比赛途中疯狂改题面,还有所谓的不大不小的模拟,简直无力吐槽了.
唯一的收获可能是学了个cbrt函数吧.
希望下一场能够正常一些.
本文地址: 2020寒假算法集训营 Day3题解

