基本概念
和常规意义下最小生成树的概念类似,该算法用于求解在二维平面上所有点的最小生成树.两点之间的距离定义为曼哈顿距离.
原理
如果使用朴素的求法,时间复杂度为
O(n^2logn)
而点的数据规模一般在1e5左右,这个复杂度是无法接受的.所以,需要根据曼哈顿距离的特殊性质,删去大量的无用边,进而优化算法.
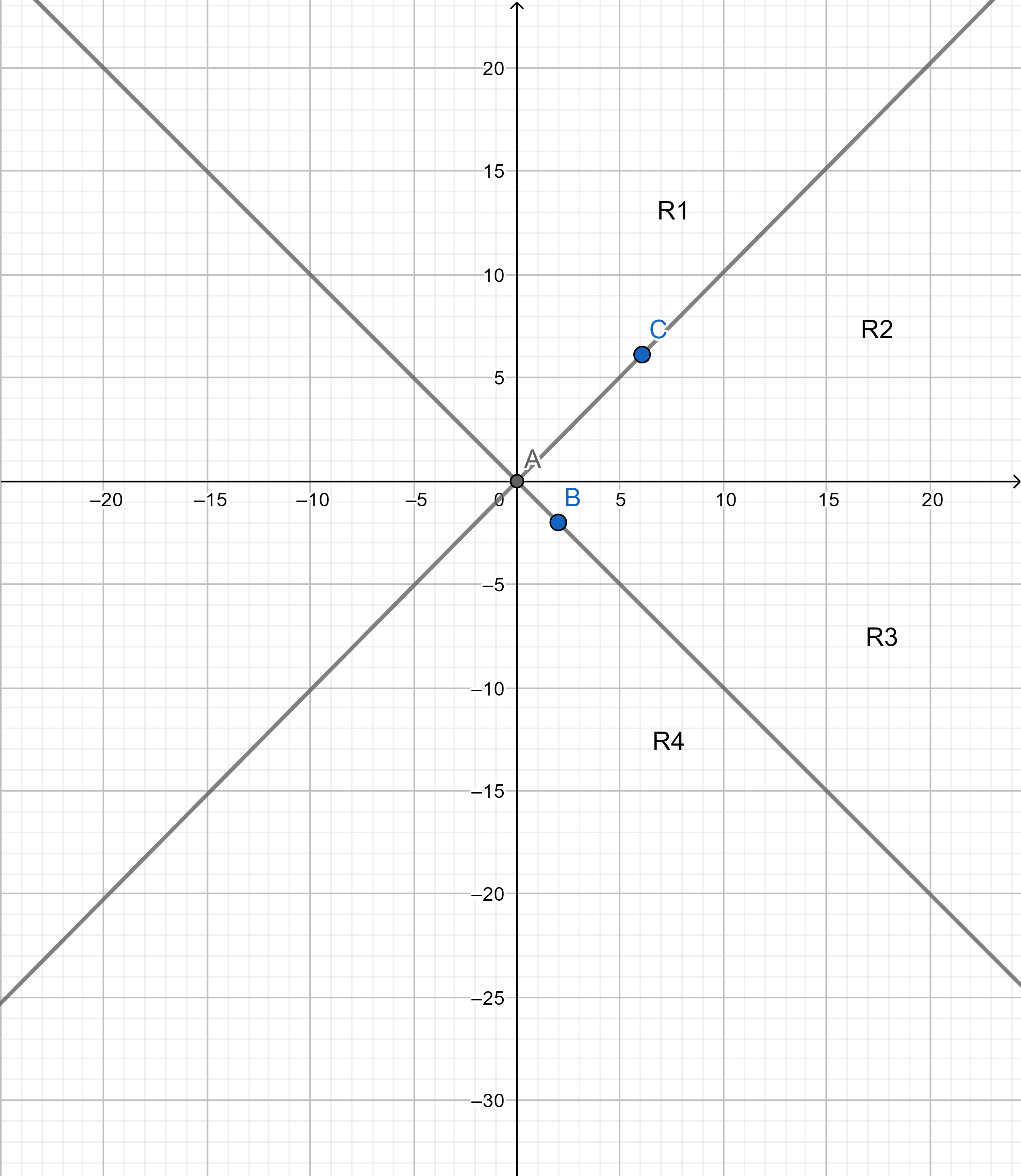
首先以任意一点为坐标原点,做出y=x和y=-x两条直线,将坐标轴分成八个部分.如下图所示:
考虑R1这一部分.如果在这一区间内存在一点P和A点的距离最小,则连接一条从A到该点的边.假如这部分里存在另外一点Q,该点到A的距离没有P到A的距离小,则不进行连边.因为有
|AP|>|AQ|->|AQ|>|PQ|
(证明略).所以在生成树上一定是P和A连边,而不是Q和A连边.
由于对称性,划分出的八个区域只需要计算上图中的四个区域即可.接下来考虑如何找出距离原点最近的点.经过推导,四个区域依次有如下条件:
x_i \leq x \ \ y_i-x_i \leq y-x
y_i \leq y \ \ y-x \leq y_i-x_i
y \leq y_i \ \ y_i+x_i \leq y+x
x_i \leq x \ \ y+x \leq y_i+x_i
(原点坐标为(x_i,y_i)),其他点坐标为(x,y)
其中第一个条件可以排序解决,第二个条件则可以使用树状数组解决.
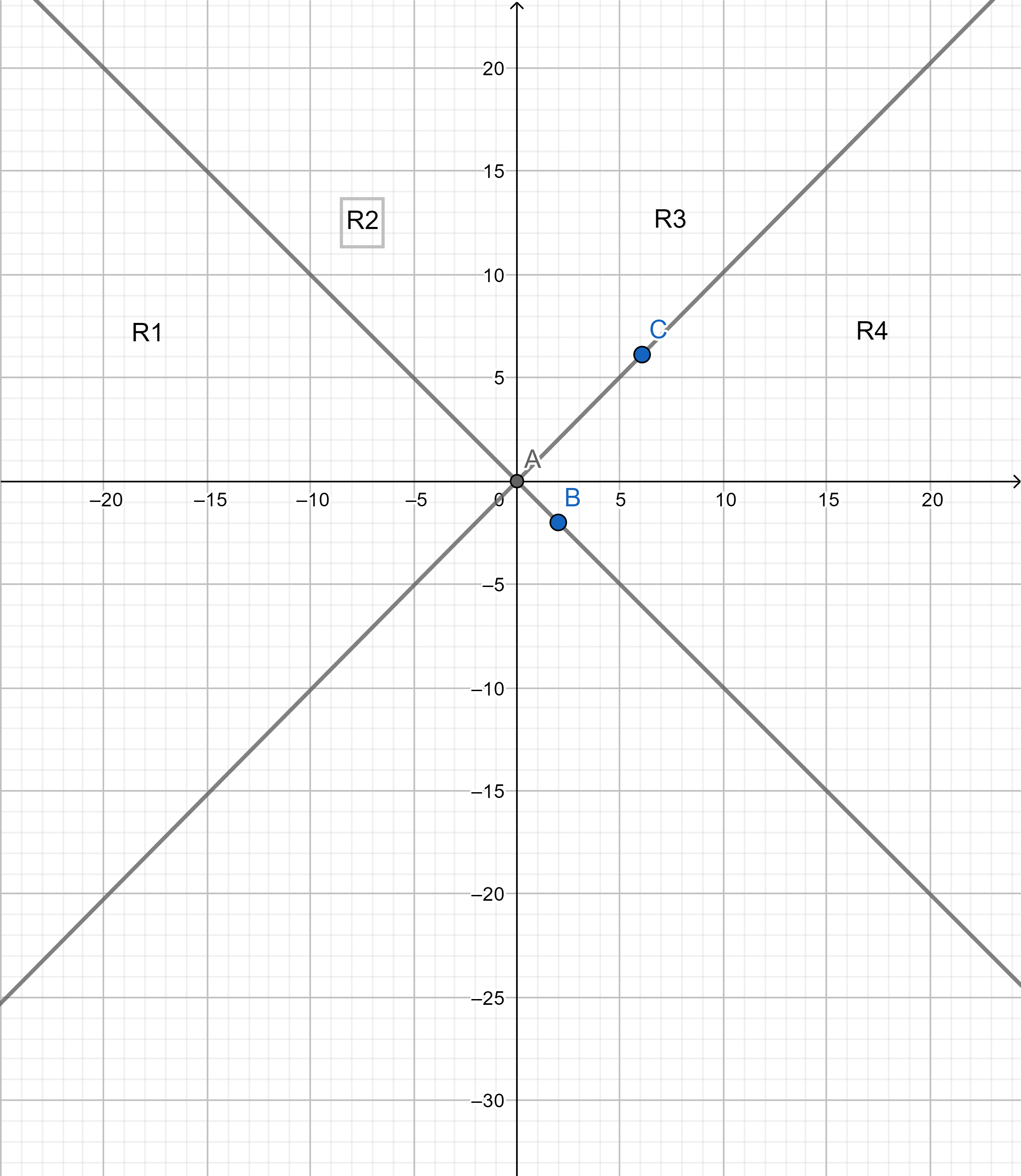
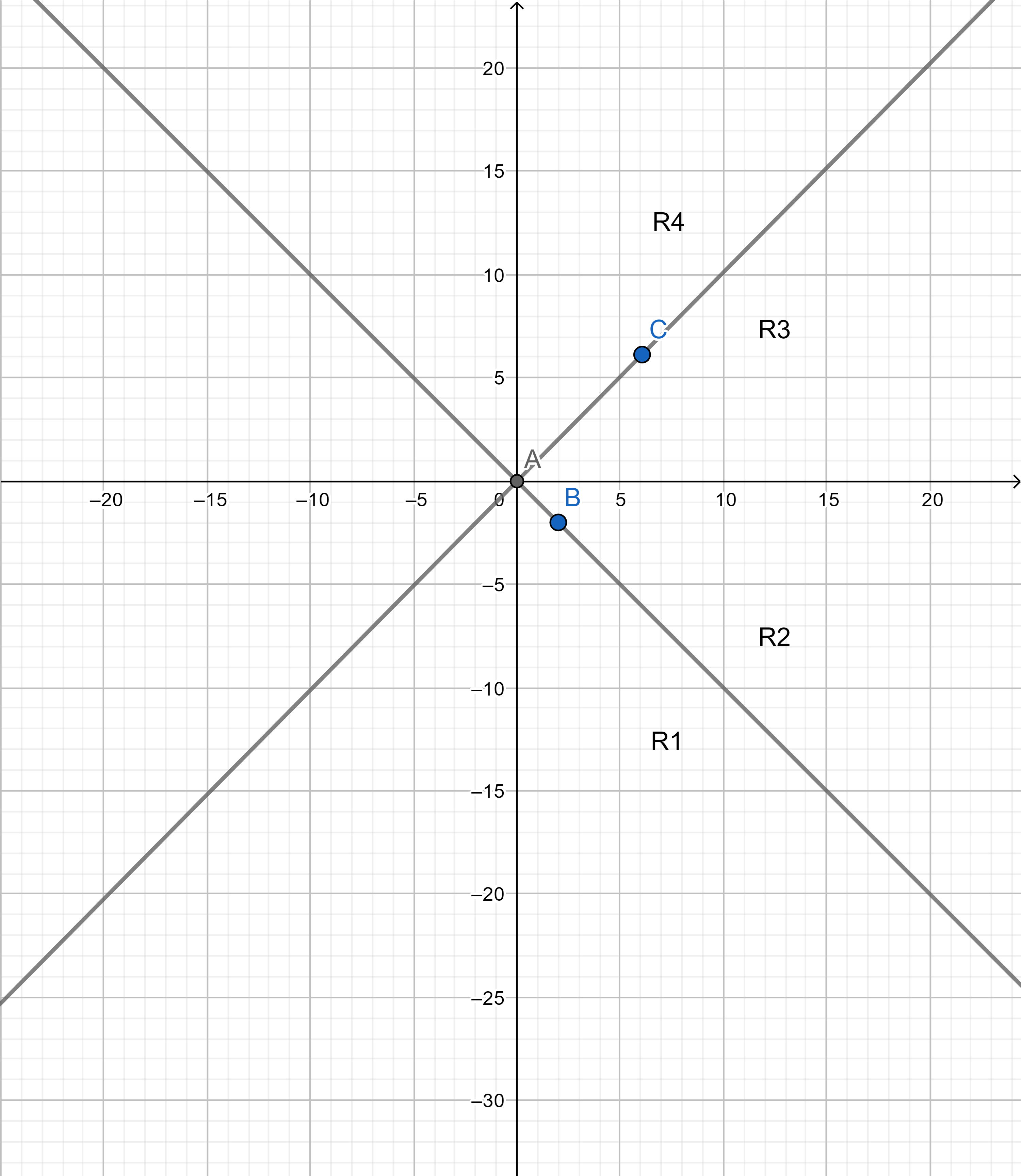
关于分别计算这四种情况有个技巧,可以通过对称变换将其转化为求R1区域的情况.如下图所示:
关于y=x对称后:
关于y轴对称后:
再关于y=x对称后:
模板
inline void Change(int l,int r,int p){
int i=0;
for (i=l;i;i-=bit(i))
if (t[i].x>r) t[i].x=r,t[i].id=p;
}
inline void Add(int s,int t,int fl){
e[lsum].x=s; e[lsum].y=t; e[lsum++].id=fl;
}
for (dir=1;dir<=4;dir++){
if ((dir%2)==0)
for (i=1;i<=n;i++) Swap(a[i].x,a[i].y);
if (dir==3)
for (i=1;i<=n;i++) a[i].x*=-1;
sort(a+1,a+1+n,cmp);
for (i=1;i<=n;i++) b[i]=a[i].y-a[i].x,l[i]=&b[i];
sort(l+1,l+1+n,Cmp);
for (i=1;i<=n;i++) *l[i]=i;
for (i=1;i<=n;i++) t[i].x=INF,t[i].id=-1;
for (i=n;i;i--){
pos=Query(b[i]);
if (pos!=-1)
Add(a[i].id,a[pos].id,Dis(i,pos));
Change(b[i],a[i].x+a[i].y,i);
}
}
例题
题意:
求曼哈顿距离最小生成树上第K大的边.
代码:
#include<cstring>
#include<cstdio>
#include<cstdlib>
#include<iostream>
#include<algorithm>
#include<vector>
#include<cmath>
#include<queue>
#include<map>
#define N 10010
#define l(x) (x<<1)
#define r(x) ((x<<1)+1)
#define bit(x) (x&(-x))
#define LL long long
#define INF 0x3f3f3f3f
using namespace std;
int n,m,i,lsum=1,dir,pos,x,y,ss;
int b[N],f[N],*l[N];
struct Data{
int x,y,id;
}a[N],t[N],e[N*8];
inline bool cmp2(Data x,Data y){return x.id<y.id;}
inline bool Cmp(const int *a,const int *b){return *a<*b;}
inline bool cmp(Data x,Data y){return (x.x==y.x)?x.y<y.y:x.x<y.x;}
inline int Abs(int x){return (x<0)?-x:x;}
inline void Swap(int &x,int &y){x^=y^=x^=y;}
inline int Min(int a,int b){return (a<b)?a:b;}
inline int Max(int a,int b){return (a>b)?a:b;}
inline int read(){
int p=0; char c=getchar();
while (c<48||c>57) c=getchar();
while (c>=48&&c<=57) p=(p<<1)+(p<<3)+c-48,c=getchar();
return p;
}
inline int Dis(int x,int y){
return Abs(a[x].x-a[y].x)+Abs(a[x].y-a[y].y);
}
inline int Query(int x){
int i=0,Ans=INF,id=-1;
for (i=x;i<=n;i+=bit(i))
if (t[i].x<Ans) Ans=t[i].x,id=t[i].id;
return id;
}
inline void Change(int l,int r,int p){
int i=0;
for (i=l;i;i-=bit(i))
if (t[i].x>r) t[i].x=r,t[i].id=p;
}
inline void Add(int s,int t,int fl){
e[lsum].x=s; e[lsum].y=t; e[lsum++].id=fl;
}
inline int Find(int x){return (x==f[x])?x:f[x]=Find(f[x]);}
int main(){
scanf("%d%d",&n,&m);
for (i=1;i<=n;i++){
scanf("%d%d",&a[i].x,&a[i].y);
a[i].id=i;
}
for (dir=1;dir<=4;dir++){
if ((dir%2)==0)
for (i=1;i<=n;i++) Swap(a[i].x,a[i].y);
if (dir==3)
for (i=1;i<=n;i++) a[i].x*=-1;
sort(a+1,a+1+n,cmp);
for (i=1;i<=n;i++) b[i]=a[i].y-a[i].x,l[i]=&b[i];
sort(l+1,l+1+n,Cmp);
for (i=1;i<=n;i++) *l[i]=i;
for (i=1;i<=n;i++) t[i].x=INF,t[i].id=-1;
for (i=n;i;i--){
pos=Query(b[i]);
if (pos!=-1)
Add(a[i].id,a[pos].id,Dis(i,pos));
Change(b[i],a[i].x+a[i].y,i);
}
}
sort(e+1,e+lsum,cmp2);
for (i=1;i<=n;i++) f[i]=i;
ss=n;
for (i=1;i<lsum;i++){
x=Find(e[i].x); y=Find(e[i].y);
if (x==y) continue;
f[x]=y; ss--;
if (ss==m) {
printf("%d\n",e[i].id); break;
}
}
return 0;
}
声明:
本文采用
BY-NC-SA
协议进行授权,如无注明均为原创,转载请注明转自
Marvolo
本文地址: 曼哈顿距离最小生成树学习笔记
本文地址: 曼哈顿距离最小生成树学习笔记