扩散模型学习笔记
模型原理
逐步加噪
对于一张图片,如果每次都在每个像素上加一点噪声,经过足够多的轮次之后,整张图片看起来几乎丢失掉了所有的信息。如果想从最后得到的噪声图直接还原到原图片,这个过程是非常困难的。但如果每次只还原一点,也就是尝试还原出一次迭代前的结果,从数学上可以证明,这种分布还原的过程是可以让神经网络学习的,这就是扩散模型的基本思路。
整个流程如下图所示:

对于前向加噪的过程,设\beta_{t}是第t次加噪的程度,并且有0<\beta_{1}<\beta_{2}<...<\beta_{n}<1;初始状态记为x_{0},则有
q(x_{t}|x_{t-1}) = N(x_{t}; \sqrt{1-\beta_{t}}x_{t-1}, \beta_{t}I)
表示x_{t}是从均值为\sqrt{1-\beta_{t}}x_{t-1},方差为\beta_{t}I的正态分布上进行的采样。但是这种形式不便于推导与训练,根据正态分布的性质,可以改写为如下形式:
q(x_{t}|x_{t-1}) = \sqrt{1-\beta_{t}}x_{t-1} + z_{t-1}\sqrt{\beta_{t}}
引入了一个新的随机变量z,其中z服从N(0,1)。
一次加噪
不难发现,这个加噪过程是一个典型的马尔科夫链,如果知道初始状态x_{0}和\beta,那么肯定是可以直接计算得到x_{t}的。
记\alpha_{t} = 1 - \beta_{t},\overline{a_{t}} = \Pi_{i=1}^{t}\alpha_{i},通过一系列推导,可以得到如下结果:
x_{t} = \sqrt{\overline{\alpha_{t}}}x_{0}+\sqrt{1-\overline{\alpha_{t}}}z
故可以记为p(x_{t}|x_{0}) = N(x_{0};\sqrt{\overline{\alpha_{t}}}x_{0},(1-\overline{\alpha_{t}})I)
借助这个结果,可以大大加快前向扩散过程。
逆向扩散
在得知了先验概率p(x_{t}|x_{t-1})的分布后,我们希望神经网络可以从中学习到后验概率p_{\theta}(x_{t-1}|x_{t})。这里做了一个很强的假设,就是这个函数同样遵循正态分布(这需要T足够大,同时个人理解也是扩散模型解释性不足的地方之一)。假设的数学描述如下:
p_{\theta}(x_{t-1}|x_{t}) = N(x_{t-1};\mu_{\theta}(x_{t},t),\Sigma_{\theta}(x_{t},t))
如果加入x_{0}作为条件,根据贝叶斯分布,有:
q(x_{t-1}|x_{t},x_{0}) = q(x_{t}|x_{t-1},x_{0})\frac{q(x_{t-1}|x_{0})}{q(x_{t}|x_{0})}
根据上面的推导过程,右面三项均服从于正态分布,所以他们的概率密度函数的乘积仍然是一个正态分布函数的概率密度函数,提取其中的系数,可以得到正态分布的相关参数:
\tilde{\beta_{t}} = \frac{1-\overline{\alpha_{t-1}}}{1-\overline{\alpha_{t}}} \beta_{t}
\tilde{\mu_{t}}(x_{t},z_{t}) = \frac{1}{\sqrt{\alpha_{t}}}(x_{t}-\frac{\beta_{t}}{\sqrt{1-\overline{\alpha_{t}}}}z_{\theta}(x_{t},t))
有了均值与方差,就可以得到扩散模型单步去噪的过程:
x_{t-1} = \frac{1}{\sqrt{\alpha_{t}}}(x_{t}-\frac{\beta_{t}}{\sqrt{1-\overline{\alpha_{t}}}}z_{\theta}(x_{t},t)) + \sqrt{\tilde{\beta_{t}}}z
上式中的z_{\theta}就是我们希望神经网络学习的部分。
损失函数
优化的目标是,使得p_{\theta}逆扩散过程得到的数据分布尽可能与q_{x_{0}}一致。可以考虑优化其负对数似然-\log p_{\theta(x_{0})},但是其无法被直接计算。
有一个间接的思路是:如果可以得到这个式子的上界,然后尝试优化使其上界尽可能地小,那么也可以达到优化原式的效果。这里采用的手法是加一个 KL 散度(KL 散度是恒大于等于0的,具体见附录):
-\log p_{\theta(x_{0})} \leq -\log p_{\theta(x_{0})} + D_{KL}(q(x_{1:T}|x_{0})||p_{\theta}(x_{1:T}|x_{0})) = E_{q}[log\frac{q(x_{1:T}|x_{0})}{p_{\theta}(x_{0:T})}]
两边同时乘以-E_{q(x_{0})},得到交叉熵形式上界:
L_{VLB} = E_{q(x_{0:T})}[log\frac{q(x_{1:T}|x_{0})}{p_{\theta}(x_{0:T})}]
经过推导,可训练的部分为:
L_{t}^{simple} = E_{x_{0},z,t}[|| z_{t}-z_{\theta}(\sqrt{\overline{\alpha_{t}}}x_{0}+\sqrt{1-\overline{\alpha_{t}}}z_{t},t) ||^{2}]
直观理解就是,预测的噪声与实际噪声的 L2 范式。
网络设计
扩散模型要求输入输出的维度相同(都是一副图像的维度),故使用的网络结构是 UNet,其结构如下图所示:
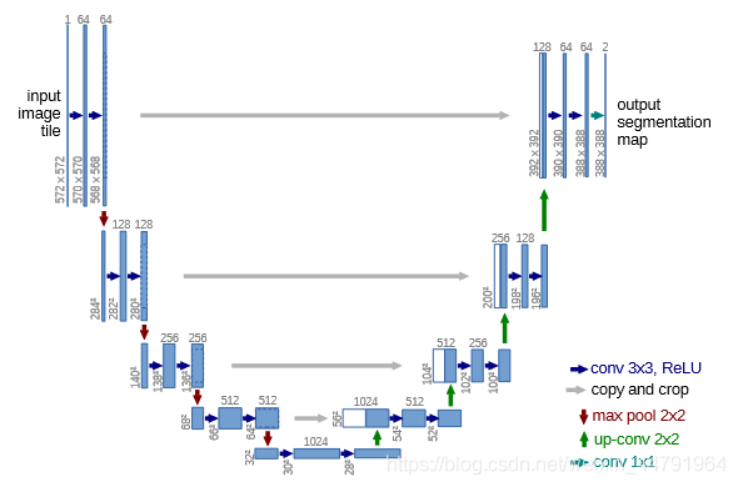
其整体结构类似于一个编码器-解码器的形式,个人理解是,前面提取特征,同时保存提取结果,然后将提取出的特征拼接到网络的后半部分,辅助进行对每个像素的分类(在扩散模型中应该是预测噪声)。
其编码器部分的示例实现如下:
def get_mobilenet_encoder( input_height=224 , input_width=224 , pretrained='imagenet' ):
alpha=1.0
depth_multiplier=1
dropout=1e-3
img_input = Input(shape=(input_height,input_width , 3 ))
x = _conv_block(img_input, 32, alpha, strides=(2, 2))
x = _depthwise_conv_block(x, 64, alpha, depth_multiplier, block_id=1)
f1 = x
x = _depthwise_conv_block(x, 128, alpha, depth_multiplier,
strides=(2, 2), block_id=2)
x = _depthwise_conv_block(x, 128, alpha, depth_multiplier, block_id=3)
f2 = x
x = _depthwise_conv_block(x, 256, alpha, depth_multiplier,
strides=(2, 2), block_id=4)
x = _depthwise_conv_block(x, 256, alpha, depth_multiplier, block_id=5)
f3 = x
x = _depthwise_conv_block(x, 512, alpha, depth_multiplier,
strides=(2, 2), block_id=6)
x = _depthwise_conv_block(x, 512, alpha, depth_multiplier, block_id=7)
x = _depthwise_conv_block(x, 512, alpha, depth_multiplier, block_id=8)
x = _depthwise_conv_block(x, 512, alpha, depth_multiplier, block_id=9)
x = _depthwise_conv_block(x, 512, alpha, depth_multiplier, block_id=10)
x = _depthwise_conv_block(x, 512, alpha, depth_multiplier, block_id=11)
f4 = x
x = _depthwise_conv_block(x, 1024, alpha, depth_multiplier,
strides=(2, 2), block_id=12)
x = _depthwise_conv_block(x, 1024, alpha, depth_multiplier, block_id=13)
f5 = x
return img_input , [f1 , f2 , f3 , f4 , f5 ]
可以看到保存中间的部分特征提取结果。在解码过程中,不断将其拼接到后方,同时对向量进行升维:
def _unet( n_classes , encoder , l1_skip_conn=True, input_height=416, input_width=608 ):
img_input , levels = encoder( input_height=input_height , input_width=input_width )
[f1 , f2 , f3 , f4 , f5 ] = levels
o = f4
# 26,26,512
o = ( ZeroPadding2D( (1,1) , data_format=IMAGE_ORDERING ))(o)
o = ( Conv2D(512, (3, 3), padding='valid', data_format=IMAGE_ORDERING))(o)
o = ( BatchNormalization())(o)
# 52,52,512
o = ( UpSampling2D( (2,2), data_format=IMAGE_ORDERING))(o)
# 52,52,768
o = ( concatenate([ o ,f3],axis=MERGE_AXIS ) )
o = ( ZeroPadding2D( (1,1), data_format=IMAGE_ORDERING))(o)
# 52,52,256
o = ( Conv2D( 256, (3, 3), padding='valid', data_format=IMAGE_ORDERING))(o)
o = ( BatchNormalization())(o)
# 104,104,256
o = ( UpSampling2D( (2,2), data_format=IMAGE_ORDERING))(o)
# 104,104,384
o = ( concatenate([o,f2],axis=MERGE_AXIS ) )
o = ( ZeroPadding2D((1,1) , data_format=IMAGE_ORDERING ))(o)
# 104,104,128
o = ( Conv2D( 128 , (3, 3), padding='valid' , data_format=IMAGE_ORDERING ) )(o)
o = ( BatchNormalization())(o)
# 208,208,128
o = ( UpSampling2D( (2,2), data_format=IMAGE_ORDERING))(o)
if l1_skip_conn:
o = ( concatenate([o,f1],axis=MERGE_AXIS ) )
o = ( ZeroPadding2D((1,1) , data_format=IMAGE_ORDERING ))(o)
o = ( Conv2D( 64 , (3, 3), padding='valid' , data_format=IMAGE_ORDERING ))(o)
o = ( BatchNormalization())(o)
o = Conv2D( n_classes , (3, 3) , padding='same', data_format=IMAGE_ORDERING )( o )
# 将结果进行reshape
o = Reshape((int(input_height/2)*int(input_width/2), -1))(o)
o = Softmax()(o)
model = Model(img_input,o)
return model
代码实现
原论文的代码是 TensorFlow 实现的,这里为了理解起来更方便,选择了别人的 Pytorch 版本。
参数准备
首先生成一个随机\beta序列,有两种方式,一种是线性生成,一种是从余弦函数上采样。
def linear_beta_schedule(timesteps):
scale = 1000 / timesteps
beta_start = scale * 0.0001
beta_end = scale * 0.02
# 这里没有使用原文的[0, 1],而是使用了自定义的范围
# 可以作为超参数进行调整
return torch.linspace(beta_start, beta_end, timesteps, dtype = torch.float64)
def cosine_beta_schedule(timesteps, s = 0.008):
"""
cosine schedule
as proposed in https://openreview.net/forum?id=-NEXDKk8gZ
"""
steps = timesteps + 1
x = torch.linspace(0, timesteps, steps, dtype = torch.float64)
alphas_cumprod = torch.cos(((x / timesteps) + s) / (1 + s) * math.pi * 0.5) ** 2
alphas_cumprod = alphas_cumprod / alphas_cumprod[0]
betas = 1 - (alphas_cumprod[1:] / alphas_cumprod[:-1])
return torch.clip(betas, 0, 0.999)
然后对要用到的参数预处理:
alphas = 1. - betas
alphas_cumprod = torch.cumprod(alphas, dim=0)
# 将之前结果累乘
alphas_cumprod_prev = F.pad(alphas_cumprod[:-1], (1, 0), value = 1.)
# 在最前面补了一个 1,抹掉了最后一项
# 做这个偏移是因为之后使用这个序列时的下标往往是 t-1
# 为了可以直接计算,做了一个拼接
register_buffer = lambda name, val: self.register_buffer(name, val.to(torch.float32))
register_buffer('betas', betas)
register_buffer('alphas_cumprod', alphas_cumprod)
register_buffer('alphas_cumprod_prev', alphas_cumprod_prev)
# calculations for diffusion q(x_t | x_{t-1}) and others
register_buffer('sqrt_alphas_cumprod', torch.sqrt(alphas_cumprod))
register_buffer('sqrt_one_minus_alphas_cumprod', torch.sqrt(1. - alphas_cumprod))
register_buffer('log_one_minus_alphas_cumprod', torch.log(1. - alphas_cumprod))
register_buffer('sqrt_recip_alphas_cumprod', torch.sqrt(1. / alphas_cumprod))
register_buffer('sqrt_recipm1_alphas_cumprod', torch.sqrt(1. / alphas_cumprod - 1))
# 前向传播用到的参数计算
之后计算后向传播用到的\tilde{\beta_{t}} = \frac{1-\overline{\alpha_{t-1}}}{1-\overline{\alpha_{t}}} \beta_{t}:
posterior_variance = betas * (1. - alphas_cumprod_prev) / (1. - alphas_cumprod)
前向传播
q_sample计算的是q(x_{t}|x_{0}),这里用到了辅助函数extract,负责提取t时刻的对应参数
def extract(a, t, x_shape):
b, *_ = t.shape
out = a.gather(-1, t)
return out.reshape(b, *((1,) * (len(x_shape) - 1)))
def q_sample(self, x_start, t, noise=None):
noise = default(noise, lambda: torch.randn_like(x_start))
return (
extract(self.sqrt_alphas_cumprod, t, x_start.shape) * x_start +
extract(self.sqrt_one_minus_alphas_cumprod, t, x_start.shape) * noise
)
然后是完整的forward过程:
def p_losses(self, x_start, t, noise = None):
b, c, h, w = x_start.shape
noise = default(noise, lambda: torch.randn_like(x_start))
# noise sample
x = self.q_sample(x_start = x_start, t = t, noise = noise)
# 只计算到传入的 t 时刻
# if doing self-conditioning, 50% of the time, predict x_start from current set of times
# and condition with unet with that
# this technique will slow down training by 25%, but seems to lower FID significantly
x_self_cond = None
if self.self_condition and random() < 0.5:
with torch.no_grad():
x_self_cond = self.model_predictions(x, t).pred_x_start
x_self_cond.detach_()
# predict and take gradient step
model_out = self.model(x, t, x_self_cond)
if self.objective == 'pred_noise':
target = noise
elif self.objective == 'pred_x0':
target = x_start
else:
raise ValueError(f'unknown objective {self.objective}')
# 计算模型的输出,有噪声和原始图片两种形式
loss = self.loss_fn(model_out, target, reduction = 'none')
loss = reduce(loss, 'b ... -> b (...)', 'mean')
loss = loss * extract(self.p2_loss_weight, t, loss.shape)
return loss.mean()
def forward(self, img, *args, **kwargs):
b, c, h, w, device, img_size, = *img.shape, img.device, self.image_size
assert h == img_size and w == img_size, f'height and width of image must be {img_size}'
t = torch.randint(0, self.num_timesteps, (b,), device=device).long()
# 这里 t 是从 0, 1000随机选取的
img = normalize_to_neg_one_to_one(img)
return self.p_losses(img, t, *args, **kwargs)
t 的取值不是 1000 而是随机数,这是因为在足够多训练轮次的时候,可以认为反向的每一步都被均匀的覆盖到了轮次/1000次,一定程度上可以减小训练量。
注意训练时用到的噪声是一次性生成t组,但前向传播的时候并不是一次次计算的,而是根据上面一步到位那个公式去计算;然后模型预测出的结果去和x_{t-1}到x_{t}用到的噪声去计算损失函数。
损失计算
原论文使用的是 L2 损失函数,但是改进版也可以使用 L1,原因是梯度更大,可以加快收敛速度:
@property
def loss_fn(self):
if self.loss_type == 'l1':
return F.l1_loss
elif self.loss_type == 'l2':
return F.mse_loss
else:
raise ValueError(f'invalid loss type {self.loss_type}')
总结
扩散模型的前向传播过程,个人理解是将一个矩阵,通过不断加高斯噪声,映射到另一个矩阵的过程,有些类似于空间中的线性变换。这一过程肯定会丢失一些信息,但图片中的部分特征被隐式的保存了下来。神经网络要学习的,就是这个线性变换的逆变换,根据这些残留的特征,推断出原始信息。同时,关系相近的一类图片在变换后应该也是相近的(例如含有猫的图片在映射后,所含有的隐式特征应该类似),所以才可以人工设置噪声图来控制生成的结果。
扩散模型同样有一定的局限性,例如训练过程过慢,可解释性有待进一步完善,最优加噪方式的选择等。在之后的文章中或许会针对上述问题以及相关论文进行进一步的深入探讨。
参考文献
扩散模型(一):DDPM 基本原理与 MegEngine 实现

