上机题目题解

电力分配

n=int(input())
a=[0 for i in range(n)]
for i in range(n):
    a[i]=int(input())
m=int(input())
b=[0 for i in range(m)]
for i in range(m):
    b[i]=int(input())
b.sort()
ans=0
for i in b:
    for j in range(n):
        if (i>=a[j]):
            ans+=1
            a[j]=0x3f3f3f3f
            break
print(ans)

这个题目有一个坑点是,给出的数据都不一定是有序的,所以在读入之后需要进行一次排序.排序完成后,从功率最低的发电机开始,按照生产线所需功率从小到大尝试给生产线供电,当发现可以满足某个生产线的需求的时候,答案+1.然后把该生产线所需功率设为一个特别大的数,避免对之后计算答案产生干扰.

在答疑的过程中发现很多人使用了pop函数来替代标程中的置为无穷的操作.这种在遍历某个可迭代对象时同时修改该可迭代对象的写法其实是一种不好的编程习惯.因为在这一过程中很可能出现下标越界或者是漏掉其中某些元素的情况.所以,在平时使用list的时候,一般只会对记录答案的,当做栈/队列使用的,或是记录中间运算结果的列表使用pop函数,对于储存了计算时需要用到的信息的列表,不要轻易使用pop函数.append函数同理.

然后解释一下上面的0x3f3f3f3f,这是一个十六进制数,其值是1061109567,经常被用作无穷大量.大部分题目中数据的最大值在10^9以内,刚好小于这个数.它还有一个非常良好的性质是,两倍的这个数是小于C/C++中的int类型的上界的,代码中假如因为某些写法发生了无穷大量相加的情况,这个数可以避免溢出的问题.因为大家在之后基本上都要学C,这种C里的技巧可以提前记一下.

我不是盘神

n=int(input())
a=[0 for i in range(n)]
for i in range(n):
    a[i]=int(input())
a.sort()
up=n//3
ans=0
for i in range(up):
    ans+=a[i]
print(ans)
for i in range(up):
    print(a[i],end=' ')

和上一题一样,读入了数据后先排序.这题的目的是让下载文件所需的时间尽可能的少,所以也是使用贪心算法.我们用X表示用Download下载文件,T表示用网盘下载文件.经过简单的思考后不难得知,最后的下载情况应该是XXTXXTXXTXX...这样的,用网盘下载来隔开两个Download下载,这样可以使得时间最小化.

很多人选择用一个list来模拟待下载文件队列,然后又根据剩余数量分情况讨论,其实不用那么麻烦的.对上面的数列分析一下就会知道,n//3就是需要使用网盘下载的文件数量.那么在排序后,直接把前n//3个文件拿出来就行了.

在写题的时候,要善用数学工具简化代码,尽量不要去模拟题意.这一点在思维试炼中会有更明显的体现.

装备选择

n=int(input())#下面会把这个问题转化为背包模型
w=[0 for i in range(n)]#物品体积
c=[0 for i in range(n)]#物品价值
for i in range(n):
    w[i],c[i]=map(int,input().split())
m=int(input())
f=[0 for i in range(m+100)]#用于dp的数组
p=[0 for i in range(m+100)]#储存选择情况的数组
for i in range(n):
    for j in range(m,w[i]-1,-1):
        if (f[j-w[i]]+c[i]>f[j]):
            f[j]=f[j-w[i]]+c[i]#更新答案
            p[j]=p[j-w[i]]|(1<<i)#更新状态
print(f[m])
cnt=0
ans=''
for i in range(n):
    if (p[m]&(1<<i)):
        cnt+=1
        ans=ans+str(i)+' '
print(cnt,ans,sep='\n')

助教碎碎念:我的几个教练教DP的时候都是拿二维状态当引子一带而过了,上来直接讲的是一维的状态描述.所以我学的背包问题都是一维的QAQ

这题就是上课讲的DP的例题,转移的方法和记录方案的方法在PPT里可以找到完整的代码.大部分人WA的点应该是方案找的不正确.

上面这段代码为什么可以用一维状态来计算答案在下面的DP内容补充中有详细的解释,这里不再赘述.重点讲一下状态的记录.当DP数组被更新之后,说明选择把某件物品放进背包,假设当前体积为i,物品体积为w.物品选择的方案就是i-w体积下物品选择的方案再加上这一件物品.

上面使用了二进制而不是list来记录选择的方案.通过或运算来把一个二进制数的特定位置置为1,最后再通过与运算来判断某一位是不是1.二进制的表达和使用技巧详见第五周周报.

我不是盘神 Pro

n=int(input())
f=[[0 for i in range(2)] for i in range(n+10)]
for i in range(2,n+2):
    x=int(input())
    f[i][0]=min(f[i-2][1],f[i-1][1])
    f[i][1]=min(f[i-1][0]+x,f[i-1][1]+x)
print(min(f[n+1][0],f[n+1][1]))

f[i][0]表示下载了前i个文件,最后一个文件是加速下载的,总共使用了多少时间;f[i][1]表示下载了前i个文件,最后一个文件是通过网盘下载的,总共使用了多少时间.为了防止溢出,下标从2开始.

然后分析一下两个转移方程:

f[i][0]=min(f[i-2][1],f[i-1][1])

如果第i个文件决定使用加速下载,那么按照题意,至多连续下载两个,所以,第i-2,i-1个文件是走网盘下载就可以保证第i个文件一定可以使用加速下载.因为下载不需要时间,取最小值就可以了.

f[i][1]=min(f[i-1][0]+x,f[i-1][1]+x)

如果第i个文件决定使用网盘下载,那么前一个文件用什么下载是无所谓的 ,于是可以直接进行转移.最后从里面找出最小值输出就行了.

DP内容补充

01背包

解DP问题时,要考虑的三个最重要的问题是状态描述,状态转移,无后效性.接下来会从这三个方面讲一下一维的背包问题.

首先是状态描述.在大多数题目中,是可以从题目要求解的答案中直接把状态给提取出来的.例如背包问题要求解的答案是一定体积的背包最多能装下多大价值的物品.分析下这句话,物品的价值总和是我们想最大化的一个指标,这个价值能有多大我们是不知道的,所以价值不可能作为DP的状态,只能作为dp数组中所储存的信息.背包的体积是确定的,可以拿来做状态.于是,可以写出下面的状态描述形式:

dp[i]表示不超过i体积的背包可以装下的最大价值.

当写出来了状态的描述后,接着考虑如何转移这个状态.设物品的体积为w,价值为c.然后按照题意尝试模拟一个物品放入背包的过程.如果想把这个物品放入体积为i的背包中,那么获得的价值应该是dp[i-w]+c.将这个值和原先的dp[i]进行比较,就完成了状态的更新:dp[i]=max(dp[i],dp[i-w]+c).

接下来尝试用代码实现这个转移的过程.首先枚举物品,依次尝试把一件物品放入背包中,可以得到如下代码:

for i in range(n):
    for j in range(w[i],m+1):
        dp[j]=max(dp[j],dp[j-w[i]]+c[i])

这时要检验一下有无后效性.假如说只有一个物品,体积为1,价值为100.上面的代码求出来的dp[m]将会是100m.这是因为,第二个循环是从小到大枚举体积的,假如说dp[1]被更新了,也就是这个物品已经放入了体积为1的背包中,在更新dp[2]的时候,就会调用之前的结果,导致这件物品被放进去了两次,然后以此类推,就会得到100m的结果.上面这段代码其实是完全背包(物品数量无限)的求解代码.如果要修改成01背包的,就要消除这个后效性.

从转移方程中可以看出,dp[j-w[i]]是会对dp[j]产生影响的,小体积会影响大体积.为了消除影响,可以先更新大体积的状态,再更新小体积的状态,修改后的代码如下:

for i in range(n):
    for j in range(m+1,w[i]-1,-1):
        dp[j]=max(dp[j],dp[j-w[i]]+c[i])

至此,后效性消除完毕,问题解决.

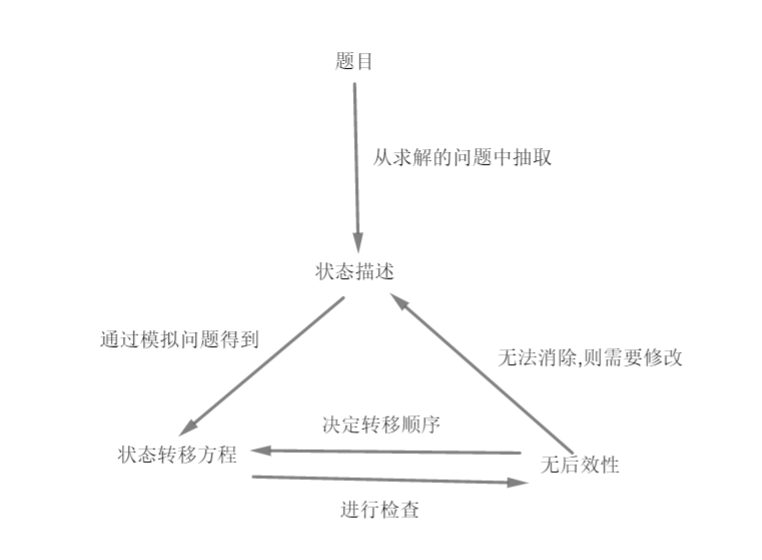
下面是我根据自己的经验得到的DP问题求解流程图:

多维DP

先看一个例题:给出一个n\times m的方格矩阵,一开始有一个人在左上角的方格,每次可以向下或者向右移动,求移动到右下角有几种方案.下面将按照上图的流程去求解这个问题.

首先,方案数是要求解的目标,不能拿来当状态.最终要的是右下角的方案数,把这个推广以下,dp[i][j]表示走到(i,j)位置的方案数,左上角是(0,0).得到了状态后,尝试去模拟题意.每一次只能向右或者向下移动,那么要走到(i,j)这个位置,只能是从(i-1,j)或(i,j-1)走过来.于是就有了状态转移方程:dp[i][j]=dp[i-1][j]+dp[i][j-1].

最后分析后效性.这个方程要需要在求dp[i][j]的时候已知dp[i-1][j]和dp[i][j-1],也就是某个位置的左上角部分区域都要求出来.dp的顺序就可以确定为从上到下,从左至右.示例代码如下:

for i in range(n):
    for j in range(m):
        if (i>0):#边界情况判断
            dp[i][j]+=dp[i-1][j]
        if (j>0):#边界情况判断
            dp[i][j]+=dp[i][j-1]

但是这样是算出来的答案会是0.原因是dp数组在一开始都是0,无论怎么求和也还是0.所以这个问题需要设置一个初始值.一开始在左上角,到左上角的方案数就是1,所以需要在开头加上一句dp[0][0]=1.

最后看一下选做题,下载时间是最小化的量,不能当状态.于是用dp[i]表示下载了i个文件所需的最小时间.然后发现题目中要求的至多用Download连续下载两个文件这个条件似乎很难满足,这个状态并不能告诉我们已经连续下载了几个文件.为了解决后效性的问题,一个常规的办法是:升维.通过升维的方法更详细地描述状态,以达到消除后效性的目的.刚刚无法解决的问题是无法得知连续下载了几个文件,那么升维后的状态可以写为dp[i][0]表示下载了i个文件,最后一个文件是用Download下载的,dp[i][1]表示下载了i个文件,最后一个文件是用网盘下载的.在此基础上再进行状态的转移.

至于升维后的状态怎么描述就比较需要经验了.这是一个需要积累的东西,大家可以在之后的做题过程中慢慢体会.