也许应该叫新学期学习计划了?
链接
题意
有n个方格,每个方格可以被染成黑色或者白色.染成黑色或白色可以获得好看度b_{i}或w_{i}.每个方格有个权值a_{i},和一个区间[l_{i},r_{i}].如果第i个方格被染成了黑色,而且存在被染成白色的方格j,满足1 \leq j
题解
基本思路是拆点,每个点拆为上下两个点,连边方案如下图:
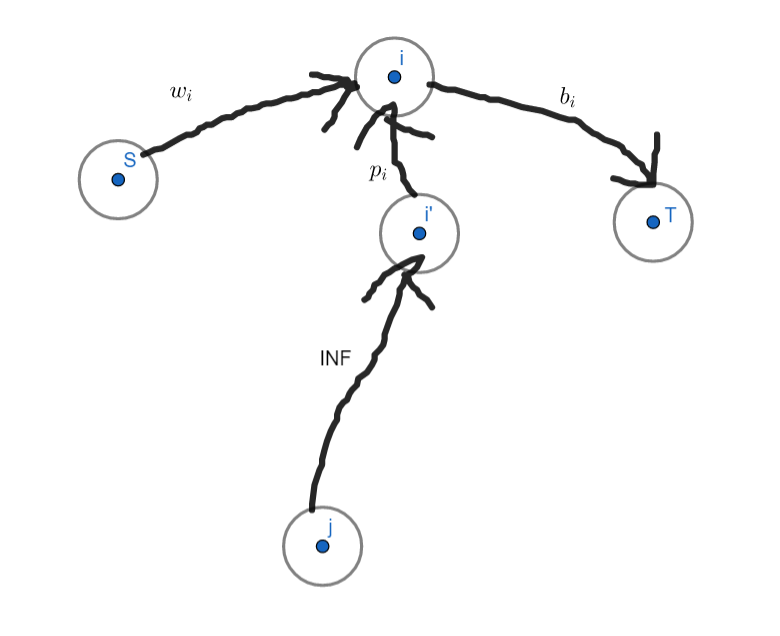
但有个问题时,这样连边的话,边数是n^{2}级的,需要进一步优化.观察一下上面的条件式,这是一个类似二维偏序的东西,所以可以考虑拿主席树优化.每次根据[l_{i},r_{i}]在主席树上查询,对应的区间向点i连边;之后再插入点i.每一个i向主席树底层的对应位置再连一条流量为INF的边,主席树上的每个节点向父节点连一条流量为INF的边.因为可能有点的权值相同,所以在创建新的叶子节点时,旧的叶子需要向新的叶子连一条流量为INF的边.优化后的边数就是nlogn级别的了,然后再跑网络流就行了.跑出来的结果是没有被选取的边以及被扣去的好看度,所以答案为\sum w_{i}+b_{i}-maxflow
代码
#include<cstring>
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<vector>
#include<cmath>
#define l(x) (x<<1)
#define r(x) ((x<<1)+1)
#define IL inline
#define reg register
#define LL long long
#define N 150010
#define INF 0x3f3f3f3f
using namespace std;
int n,i,lsum=1,cnt,Found,b,w,Ans,flow,al;
int head[N],gap[N],gaps[N],l[N],r[N],a[N],p[N],root[N];
vector <int> S;
struct Flow{
int t,next,fl,re;
}e[N*8];
struct Tree{
int l,r;
}t[N*8];
IL int Abs(int x){return (x<0)?-x:x;}
IL void Swap(int &a,int &b){a^=b^=a^=b;}
IL int Min(int a,int b){return (a<b)?a:b;}
IL int Max(int a,int b){return (a>b)?a:b;}
IL int read(){
int p=0,f=1; char c=getchar();
while (c<48||c>57) {if (c=='-') f=-1; c=getchar();}
while (c>=48&&c<=57) p=(p<<1)+(p<<3)+c-48,c=getchar();
return p*f;
}
IL void Add(int s,int t,int fl){
e[lsum].t=t; e[lsum].fl=fl; e[lsum].next=head[s]; e[lsum].re=lsum+1; head[s]=lsum++;
e[lsum].t=s; e[lsum].fl=0; e[lsum].next=head[t]; e[lsum].re=lsum-1; head[t]=lsum++;
}
IL void Sap(int x){
int i=0,mingap=cnt-1,F=al;
if (x==2*n+2) {Found=1; flow+=al; return;}
for (i=head[x];i;i=e[i].next)
if (e[i].fl){
if (gap[e[i].t]+1==gap[x]){
al=Min(al,e[i].fl); Sap(e[i].t);
if (gap[1]>=cnt) return;
if (Found) break;
al=F;
}
mingap=Min(mingap,gap[e[i].t]);
}
if (!Found){
gaps[gap[x]]--; if (!gaps[gap[x]]) gap[1]=cnt;
gaps[gap[x]=mingap+1]++;
} else e[i].fl-=al,e[e[i].re].fl+=al;
}
IL void Add_Edge(int x,int tl,int tr,int low,int high,int id){
int mid=(tl+tr)>>1;
if (!x) return;
if (tl==low && tr==high){
Add(x,id,INF); return;
}
if (high<=mid) Add_Edge(t[x].l,tl,mid,low,high,id);
else if (low>mid) Add_Edge(t[x].r,mid+1,tr,low,high,id);
else Add_Edge(t[x].l,tl,mid,low,mid,id),Add_Edge(t[x].r,mid+1,tr,mid+1,high,id);
}
IL int Insert(int pre,int low,int high,int val,int id){
int x=++cnt,mid=(low+high)>>1;
t[x]=t[pre];
if (low==high) {
Add(id,x,INF);
if (pre) Add(pre,x,INF);
return x;
}
(val<=mid)?t[x].l=Insert(t[x].l,low,mid,val,id):t[x].r=Insert(t[x].r,mid+1,high,val,id);
if (t[x].l) Add(t[x].l,x,INF);
if (t[x].r) Add(t[x].r,x,INF);
return x;
}
int main(){
#ifdef __Marvolo
freopen("zht.in","r",stdin);
freopen("zht.out","w",stdout);
#endif
n=read();
for (i=1;i<=n;i++){
a[i]=read(); b=read(); w=read();
l[i]=read(); r[i]=read(); p[i]=read();
Ans+=b+w;
Add(1,1+i,w); Add(1+i,2*n+2,b); Add(1+n+i,1+i,p[i]);
S.push_back(a[i]); S.push_back(l[i]); S.push_back(r[i]);
}
sort(S.begin(),S.end());
S.erase(unique(S.begin(),S.end()),S.end());
for (i=1;i<=n;i++){
a[i]=lower_bound(S.begin(),S.end(),a[i])-S.begin()+1;
l[i]=lower_bound(S.begin(),S.end(),l[i])-S.begin()+1;
r[i]=lower_bound(S.begin(),S.end(),r[i])-S.begin()+1;
}
cnt=2*n+2;
for (i=1;i<=n;i++){
Add_Edge(root[i-1],1,S.size(),l[i],r[i],1+n+i);
root[i]=Insert(root[i-1],1,S.size(),a[i],i+1);
}
gaps[0]=cnt;
while (gap[1]<cnt){
Found=0; al=INF; Sap(1);
}
cout<<Ans-flow<<endl;
return 0;
}
声明:
本文采用
BY-NC-SA
协议进行授权,如无注明均为原创,转载请注明转自
Marvolo
本文地址: A+B problem-主席树+网络流
本文地址: A+B problem-主席树+网络流

