比赛地址
[A]Rearranging a Sequence
题意
给出一个1~n的序列,每次把指定的一个元素提到最前面,求所有操作结束后的序列.
题解
签到题
话说这不是和前两天网络赛的题一样吗
代码
#include<cstring>
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cmath>
using namespace std;
struct point {
int val, pl;
}s[200005];
int n, m, a;
bool cmp(point a, point b) {
if (a.pl > b.pl) return true;
if (a.pl < b.pl) return false;
return a.val < b.val;
}
int main(){
cin >> n >> m;
for (int i = 1; i <= n; i++) {
s[i].val = i;
s[i].pl = 0;
}
for (int i = 1; i <= m; i++) {
scanf("%d", &a);
s[a].pl = i;
}
sort(s+1, s+n+1, cmp);
for (int i = 1; i <= n; i++) printf("%d\n", s[i].val);
return 0;
}
[B]
题意
给出一种基于异或的加密方式,然后给出一个密码表.求有多少ID序列是这个密码表无法检测到的.(原题题意过长,大概就这个意思)
题解
签到题
代码
#include<cstring>
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cmath>
using namespace std;
int ans, s[15][15];
int main(){
for (int i = 0; i <= 9; i++) for (int j = 0; j <= 9; j++) {
scanf("%d", &s[i][j]);
}
for (int k = 0; k <= 9999; k++) {
int a = k/1000, b = k/100%10, c = k/10%10, d = k%10;
int e = s[s[s[s[0][a]][b]][c]][d];
int now = 0;
for (int t = 0; t <= 9; t++) if (s[s[s[s[s[0][t]][b]][c]][d]][e] == 0) now++;
for (int t = 0; t <= 9; t++) if (s[s[s[s[s[0][a]][t]][c]][d]][e] == 0) now++;
for (int t = 0; t <= 9; t++) if (s[s[s[s[s[0][a]][b]][t]][d]][e] == 0) now++;
for (int t = 0; t <= 9; t++) if (s[s[s[s[s[0][a]][b]][c]][t]][e] == 0) now++;
for (int t = 0; t <= 9; t++) if (s[s[s[s[s[0][a]][b]][c]][d]][t] == 0) now++;
if (a != b) if (s[s[s[s[s[0][b]][a]][c]][d]][e] == 0) now++;
if (b != c) if (s[s[s[s[s[0][a]][c]][b]][d]][e] == 0) now++;
if (c != d) if (s[s[s[s[s[0][a]][b]][d]][c]][e] == 0) now++;
if (d != e) if (s[s[s[s[s[0][a]][b]][c]][e]][d] == 0) now++;
if (now > 5) ans++;
}
cout << ans << endl;
return 0;
}
[C]
题意
已知有n个传送带平行放置,传送带的一端会源源不断地出现货物,另一端依次放着n个仓库.然后有m个机械手臂分布在相邻的两个传送带之间,每个机械手臂有一个坐标,当一个货物传送到机械手臂处时,手臂可以选择把这个货物搬到相邻的传送带去.这种搬运关系是双向的.求每个仓库分别能接收到多少来及不同传送带的货物.
题解
首先对机械手臂坐标离散化,然后记录下每个传送带能向下一个传送带搬运货物的机械手臂的坐标,以及向上搬运货物的机械手臂坐标,对这些坐标分别排序.
之后考虑每个传送带对仓库的贡献.枚举一个传送带可以使用的向下搬运货物的机械手臂坐标中最小的一个,然后向下查找,每次选取可以使用的机械手臂中坐标最小的一个,直到不存在向下的机械手臂或者不能借助机械手臂向下搬运.同理,再向上查找一遍.得到了每个传送带向上向下到达的最远距离后,拿线段树区间加1.
同时,在查找的过程中要记忆化一下,在找到能向下到达的最远的传送带后,要在刚刚走过的路径上做上标记,这样就保证了查找的时间复杂度是O(m)的.总的时间复杂度为
O(m+n\log n)
其实也可以不用线段树,因为仅存在区间加1和最后的单点查询操作,完全可以使用差分来实现这一过程.这样总的时间复杂度就是线性的了.
代码
线段树版本:
#include<cstring>
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<vector>
#include<cmath>
#define N 400010
#define l(x) (x<<1)
#define r(x) ((x<<1)+1)
#define LL long long
#define INF 0x3f3f3f3f
using namespace std;
struct Data{
int x,y;
};
int n,m,i;
int *ll[N];
int x[N],y[N];
vector <int> l[N],s[N],up[N],down[N];
vector <Data> v;
struct Tree{
int l,r,d,lz;
}t[N*8];
inline int Abs(int x){return (x<0)?-x:x;}
inline void Swap(int &a,int &b){a^=b^=a^=b;}
inline int Min(int a,int b){return (a<b)?a:b;}
inline int Max(int a,int b){return (a>b)?a:b;}
inline bool cmp(const int *a,const int *b){return (*a<*b);}
inline int read(){
int p=0; char c=getchar();
while (c<48||c>57) c=getchar();
while (c>=48&&c<=57) p=(p<<1)+(p<<3)+c-48,c=getchar();
return p;
}
inline void Maketree(int x,int low,int high){
int mid=(low+high)>>1;
t[x].l=low; t[x].r=high;
if (low==high) return;
Maketree(l(x),low,mid); Maketree(r(x),mid+1,high);
}
inline void Push(int x){
int p=t[x].lz;
t[l(x)].d+=p; t[r(x)].d+=p;
t[l(x)].lz+=p; t[r(x)].lz+=p;
t[x].lz=0;
}
inline void Add(int x,int low,int high){
int mid=(t[x].l+t[x].r)>>1;
if (t[x].l==low&&t[x].r==high) {t[x].d++,t[x].lz++; return;}
if (t[x].lz) Push(x);
if (high<=mid) Add(l(x),low,high);
else if (low>mid) Add(r(x),low,high);
else Add(l(x),low,mid),Add(r(x),mid+1,high);
}
inline int Query(int x,int low){
int mid=(t[x].l+t[x].r)>>1;
if (t[x].l==t[x].r) return t[x].d;
if (t[x].lz) Push(x);
if (low<=mid) return Query(l(x),low);
else return Query(r(x),low);
}
inline void Ready(){
int i=0,j=0,k=0,w=0,r=0;
for (i=n-1;i;i--){
v.clear();
if (!l[i].size()) continue;
w=l[i][0]; r=i+1; v.push_back((Data){i,0});
for (j=i+1;j<=n;j++){
if (!l[j].size()) {r=j; break;}
if (l[j][l[j].size()-1]<=w) {r=j; break;}
for (k=0;k<l[j].size();k++){
if (l[j][k]<=w) continue;
if (down[j][k]) {r=down[j][k]; goto END;}
w=l[j][k]; v.push_back((Data){j,k}); break;
}
}
END:
for (j=0;j<v.size();j++) down[v[j].x][v[j].y]=r;
Add(1,i+1,r);
}
for (i=2;i<=n;i++){
v.clear();
if (!s[i].size()) continue;
w=s[i][0]; r=i-1; v.push_back((Data){i,0});
for (j=i-1;j;j--){
if (!s[j].size()) {r=j; break;}
if (s[j][s[j].size()-1]<=w) {r=j; break;}
for (k=0;k<s[j].size();k++){
if (s[j][k]<=w) continue;
if (up[j][k]) {r=up[j][k]; goto END2;}
w=s[j][k]; v.push_back((Data){j,k}); break;
}
}
END2:
for (j=0;j<v.size();j++) up[v[j].x][v[j].y]=r;
Add(1,r,i-1);
}
}
int main(){
scanf("%d%d",&n,&m);
for (i=1;i<=m;i++){
scanf("%d%d",&x[i],&y[i]);
ll[i]=&x[i];
}
sort(ll+1,ll+1+m,cmp);
for (i=1;i<=m;i++) *ll[i]=i;
for (i=1;i<=m;i++){
l[y[i]].push_back(x[i]); s[y[i]+1].push_back(x[i]);
down[y[i]].push_back(0); up[y[i]+1].push_back(0);
}
for (i=1;i<=n;i++){
sort(l[i].begin(),l[i].end());
sort(s[i].begin(),s[i].end());
}
Maketree(1,1,n);
Ready();
for (i=1;i<=n;i++)
printf("%d ",Query(1,i)+1);
return 0;
}
差分版本:
#include<cstring>
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<vector>
#include<cmath>
#define N 400010
#define l(x) (x<<1)
#define r(x) ((x<<1)+1)
#define LL long long
#define INF 0x3f3f3f3f
using namespace std;
struct Data{
int x,y;
};
int n,m,i,Ans;
int *ll[N];
int x[N],y[N],ans[N];
vector <int> l[N],s[N],up[N],down[N];
vector <Data> v;
inline int Abs(int x){return (x<0)?-x:x;}
inline void Swap(int &a,int &b){a^=b^=a^=b;}
inline int Min(int a,int b){return (a<b)?a:b;}
inline int Max(int a,int b){return (a>b)?a:b;}
inline bool cmp(const int *a,const int *b){return (*a<*b);}
inline int read(){
int p=0; char c=getchar();
while (c<48||c>57) c=getchar();
while (c>=48&&c<=57) p=(p<<1)+(p<<3)+c-48,c=getchar();
return p;
}
inline void Ready(){
int i=0,j=0,k=0,w=0,r=0;
for (i=n-1;i;i--){
v.clear();
if (!l[i].size()) continue;
w=l[i][0]; r=i+1; v.push_back((Data){i,0});
for (j=i+1;j<=n;j++){
if (!l[j].size()) {r=j; break;}
if (l[j][l[j].size()-1]<=w) {r=j; break;}
for (k=0;k<l[j].size();k++){
if (l[j][k]<=w) continue;
if (down[j][k]) {r=down[j][k]; goto END;}
w=l[j][k]; v.push_back((Data){j,k}); break;
}
}
END:
for (j=0;j<v.size();j++) down[v[j].x][v[j].y]=r;
ans[i+1]++; ans[r+1]--;
}
for (i=2;i<=n;i++){
v.clear();
if (!s[i].size()) continue;
w=s[i][0]; r=i-1; v.push_back((Data){i,0});
for (j=i-1;j;j--){
if (!s[j].size()) {r=j; break;}
if (s[j][s[j].size()-1]<=w) {r=j; break;}
for (k=0;k<s[j].size();k++){
if (s[j][k]<=w) continue;
if (up[j][k]) {r=up[j][k]; goto END2;}
w=s[j][k]; v.push_back((Data){j,k}); break;
}
}
END2:
for (j=0;j<v.size();j++) up[v[j].x][v[j].y]=r;
ans[r]++; ans[i]--;
}
}
int main(){
scanf("%d%d",&n,&m);
for (i=1;i<=m;i++){
scanf("%d%d",&x[i],&y[i]);
ll[i]=&x[i];
}
sort(ll+1,ll+1+m,cmp);
for (i=1;i<=m;i++) *ll[i]=i;
for (i=1;i<=m;i++){
l[y[i]].push_back(x[i]); s[y[i]+1].push_back(x[i]);
down[y[i]].push_back(0); up[y[i]+1].push_back(0);
}
for (i=1;i<=n;i++){
sort(l[i].begin(),l[i].end());
sort(s[i].begin(),s[i].end());
}
Ready();
for(i=1;i<=n;i++){
Ans+=ans[i];
printf("%d\n",Ans+1);
}
return 0;
}
[D]
题意
给出两个字符串,然后在每个串选取固定长度的一个连续子串,当且仅当两个子串所含的字母种类以及数量完全相同时则称这两个子串相同.求最长的相同子串的长度是多少.
题解
字符串Hash.预处理出每个串各个子串的哈希值,然后取最长的发生碰撞的子串长度即可.
代码
#include <iostream>
#include <cstdio>
#include <cstring>
#include <unordered_map>
#define ULL unsigned long long
constexpr int ML(5007);
#define MIN(a, b) ((a)<(b)?(a):(b))
#define MAX(a, b) ((a)>(b)?(a):(b))
ULL __r_ = 0x3badf00d3badf00d;
#define rander() (__r_+=__r_<<2ull|1ull)
ULL hashcode(int *cnt)
{
ULL hs = 0x3badf00d;
for (int len=0; len<26; ++len)
hs *= 131, hs += cnt[len];
return hs;
}
std::unordered_map<ULL, int> mp;
int main()
{
char s[ML], t[ML];
scanf("%s %s", s, t);
int matched = -1;
int len1 = strlen(s), len2 = strlen(t), mlen = MIN(len1, len2);
for (int len=1; len<=mlen; len++)
{
mp.clear();
int cnt[27] = {0};
for (int i=0; i<len; ++i)
cnt[s[i]-'a']++;
for (int i=0, ub=len1-len; i<ub; ++i)
{
++mp[hashcode(cnt)];
--cnt[s[i]-'a'], ++cnt[s[i+len]-'a'];
}
++mp[hashcode(cnt)];
memset(cnt, 0, sizeof(cnt));
for (int i=0; i<len; ++i)
++cnt[t[i]-'a'];
for (int i=0, ub=len2-len; i<ub; ++i)
{
if (mp.count(hashcode(cnt)))
matched = MAX(matched, len);
--cnt[t[i]-'a'], ++cnt[t[i+len]-'a'];
}
if (mp.count(hashcode(cnt)))
matched = MAX(matched, len);
}
if (~matched)
printf("%d", matched);
else
puts("0");
#ifdef _KEVIN
system("pause");
#endif
return 0;
}
[E]
题意
给出一个仅由+,-,*,(,),0,1,=构成的二进制等式,等式的各个符号被不同的字母替代了.现给出替代后的等式,求有多少种原等式构造方案.
题解
当字母总数大于8时无解.之后枚举上面的八种符号的排列,和字母构成对应关系,再代入等式中检验合法性以及两端是否相等即可.
代码
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cctype>
namespace kstd
{
template <typename E>
bool next_permutation(E *begin, E *end)
{
E *now = end-1, *prev = now-1, tp;
while (now > begin && *prev >= *now) // <时退出,找第一个相邻顺序对,记下prev
--now, --prev;
if (now <= begin)
return false; // 找不到,说明整体是递减的,不存在下一个排列,返回false
for (now = end-1; *now <= *prev; now--);// >时退出,从后往前找第一个大于(也是数值最小的)*prev的元素
tp = *now, *now = *prev, *prev = tp; // 然后把它和*prev交换
for (++prev, --end; prev<end; prev++,end--) // 翻转后面这部分
tp = *end, *end = *prev, *prev = tp;
return true;
}
}
constexpr int MN(50);
char op[8] = {'(', ')', '*', '+', '-', '0', '1', '='};
struct Node
{
char *s;
int v;
Node(void) { }
Node(char *ss, int vv) :
s(ss), v(vv) { }
inline char operator [](const int alpha_cnt) const
{
return s[alpha_cnt];
}
};
const Node INVALID_FLAG(nullptr, 0);
Node quation(char *s);
Node expr(char *s);
Node term(char *s);
Node factor(char *s);
Node number(char *s);
Node base(char *s);
Node quation(char* s)
{
Node left = expr(s);
if (left.s==nullptr || left[0]!='=')
return INVALID_FLAG;
Node right = expr(left.s + 1);
if (right.s==nullptr || right[0]!=0 || right.v != left.v)
return INVALID_FLAG;
return right;
}
Node expr(char *s)
{
Node ret = term(s);
if (ret.s == nullptr)
return INVALID_FLAG;
while (ret[0]=='+' || ret[0]=='-')
{
Node next = term(ret.s + 1);
if (next.s == nullptr)
return INVALID_FLAG;
ret.v += ret[0]=='+' ? next.v : -next.v;
ret.s = next.s;
}
return ret;
}
Node term(char *s)
{
Node ret = factor(s);
if (ret.s == nullptr)
return INVALID_FLAG;
while (ret[0] == '*')
{
Node next = term(ret.s + 1);
if (next.s == nullptr)
return INVALID_FLAG;
ret.v *= next.v;
ret.s = next.s;
}
return ret;
}
Node factor(char *s)
{
Node ret = INVALID_FLAG;
if (s[0] == '-')
{
ret = factor(s+1);
if (ret.s==nullptr)
return INVALID_FLAG;
ret.v *= -1;
}
else if (s[0] == '(')
{
ret = expr(s+1);
if (ret.s==nullptr || ret[0]!=')')
return INVALID_FLAG;
++ret.s; // ')'
}
else
ret = number(s);
return ret;
}
#define is01(ch) ((ch)=='0' or (ch)=='1')
Node number(char *s)
{
Node ret(s, 0);
if (!is01(*s))
return INVALID_FLAG;
if (*s=='0' && isdigit(*(s + 1)))
return INVALID_FLAG;
while (is01(*s))
{
ret.v <<= 1;
ret.v += *s++ - '0';
}
ret.s = s;
return ret;
}
int main()
{
char str[MN] = "", buf[MN] = "";
scanf("%s", str);
int len = strlen(str);
int hs[288] = {0}, alpha_cnt = 0;
for (int i=0; i<len; ++i)
if (isalpha(str[i]) && !hs[str[i]])
hs[str[i]] = ++alpha_cnt;
if (alpha_cnt > 8)
return puts("0") * 0;
long long FAC = 1;
for (int i=1, ub=8-alpha_cnt; i<=ub; ++i)
FAC *= i;
long long tot = 0;
do
{
for (int i=0; i<len; ++i)
{
if (isalpha(str[i]))
buf[i] = op[hs[str[i]] - 1];
else
buf[i] = str[i];
}
if (quation(buf).s)
++tot;
} while (kstd::next_permutation(op, op+8));
printf("%lld\n", tot / FAC);
#ifdef _KEVIN
system("pause");
#endif
return 0;
}
[I]
题意
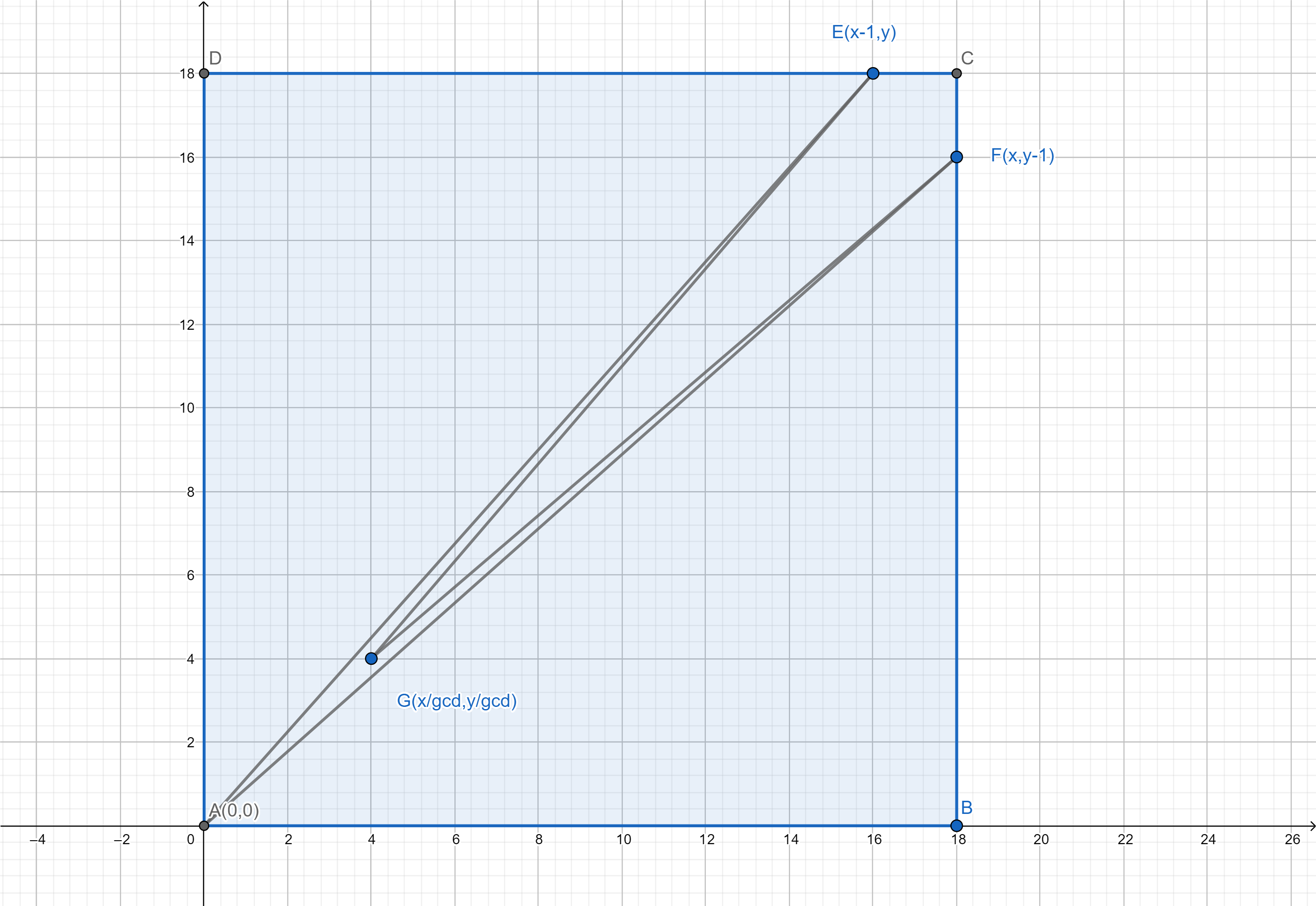
给出两个数x,y.要求构造一个三角形或者四边形,对于每个点的坐标的限制如下:
0\leq x_i \leq x
0\leq y_i \leq y
\exists x_i = x
\exists x_i = 0
\exists y_i = y
\exists y_i = 0
而且要求这个多边形的面积小于25000.求一种构造方案.
题解
当x,y过小时,可以随意构造.当x,y过大时,可以先把一个点放在原点,另一个点放在右上角,这样后面四个限制条件就满足了.接下来考虑如何放置第三个点使得面积最小就行了.
考虑gcd(x,y).当gcd(x,y)>50000时,说明x,y足够大,这时对构造方案进行微调,方案如下:
当gcd(x,y)小于50000时,这时候想办法构造一个三角形.设第三个点的坐标为(a,b),则用叉积算出的三角形面积的两倍为
bx-ay=S \leq 50000
这个时候拿拓展欧几里得直接解方程就行了,算出来的面积一定是小于25000.
代码
#include<cstring>
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cmath>
#include<cstdlib>
#include<ctime>
using namespace std;
long long int up = 50000;
int n;
long long int x, y, g;
long long int gcd(long long int x, long long int y) {
if (y == 0) return x;
return gcd(y, x%y);
}
long long int llmax(long long int a, long long int b) {
if (a > b) return a;
return b;
}
long long int exgcd(long long int a, long long int b, long long int &x, long long int &y) {
if (b == 0) { x = 1, y = 0; return a; } else {
long long int res = exgcd(b, a%b, x, y);
long long int t = x; x = y; y = t - (a/b)*y;
return res;
}
}
int main(){
cin >> n;
srand(time(NULL));
while(n--) {
scanf("%lld%lld", &x, &y);
//x = rand()%100000, y = rand()%100000;
//x = (x*10000) + rand()%10000;
//y = (y*10000) + rand()%10000;
long long int x1, y1;
g = gcd(x, y);
if (g != 1) {
long long int ans = 0;
long long int nx = x/g, ny = y/g;
x1 = x-1, y1 = y;
ans += llmax(nx*y1-ny*x1, ny*x1-nx*y1);
x1 = x, y1 = y-1;
ans += llmax(nx*y1-ny*x1, ny*x1-nx*y1);
if (ans <= up) {
printf("4\n");
printf("%lld %lld\n0 0\n", x-1, y);
printf("%lld %lld\n%lld %lld\n", x, y-1, nx, ny);
continue;
}
}
long long int nx = x/g, ny = y/g;
long long int a, b;
exgcd(nx, ny, a, b);
//x y = maxx maxy
x ^= y ^= x ^= y;
if (b>0){
int t=(b/nx);
b-=nx*t;
a+=ny*t;
if (b==0) b-=nx,a+=ny;
} else if (a>x){
int t=(a-x)/ny;
a-=t*ny; b+=t*nx;
// if (a==nx) a-=ny,b+=nx;
} else if (-b>y){
int t=(-b-y)/nx;
a-=t*ny; b+=t*nx;
// if (-b==ny) a-=ny,b+=nx;
}
x ^= y ^= x ^= y;
printf("3\n");
printf("0 0\n%lld %lld\n%lld %lld\n", x, y, llmax(b, -b), llmax(a, -a));
//long long int newans = a*x+b*y;
//if (newans > up) printf("wrong ans\n");
//printf("wrong answer : ans = %lld\n", newans);
//printf("%lld %lld\n", x, y);
//break;
}
return 0;
}
总结&吐槽
这场比赛发挥有些失常了.前期准确的判断出C题是一个水题而且是线段树之后我就开始写,中间思路变更数次,好在大方向是对的.然后就是漫长的WA和Debug时间.最后在接近四个小时的时候,把队友当做小黄鸭讲了一遍代码逻辑就发现了问题...造成的结果就是I题因为我参与的比较晚,导致之前一直在从几何的角度去解决,然后还间接导致了G题没有写完...如果G题可以顺利做出来的话就翻盘了.下一场比赛是网络赛,也是暑期集训的最后一场.即使知道即便拿第一也很难进队,毕竟前面的六支老队的实力实在是强悍,但还是希望后天的比赛可以好好发挥,把应该拿下的题目都拿下,尽量减少罚时,少口胡假算法,给暑期集训画上圆满地句号.
本文地址: ACM暑期集训第十一场