KNN部分
基础实现
首先是完善k_nearest_neighbor.py中的四个函数,其中三个函数用于计算测试集和训练集两两之间的L_{2}距离,限制条件分别是使用2个,1个,0个循环。
使用2个循环的写法最为简单:
def compute_distances_two_loops(self, X):
"""
Compute the distance between each test point in X and each training point
in self.X_train using a nested loop over both the training data and the
test data.
Inputs:
- X: A numpy array of shape (num_test, D) containing test data.
Returns:
- dists: A numpy array of shape (num_test, num_train) where dists[i, j]
is the Euclidean distance between the ith test point and the jth training
point.
"""
num_test = X.shape[0]
num_train = self.X_train.shape[0]
dists = np.zeros((num_test, num_train))
for i in range(num_test):
for j in range(num_train):
#####################################################################
# TODO: #
# Compute the l2 distance between the ith test point and the jth #
# training point, and store the result in dists[i, j]. You should #
# not use a loop over dimension, nor use np.linalg.norm(). #
#####################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
dists[i,j] = np.sum((X[i]-self.X_train[j])**2)
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
return dists
直接按照定义计算即可。
使用1重循环的写法则需要按行做一个求和:
def compute_distances_one_loop(self, X):
"""
Compute the distance between each test point in X and each training point
in self.X_train using a single loop over the test data.
Input / Output: Same as compute_distances_two_loops
"""
num_test = X.shape[0]
num_train = self.X_train.shape[0]
dists = np.zeros((num_test, num_train))
for i in range(num_test):
#######################################################################
# TODO: #
# Compute the l2 distance between the ith test point and all training #
# points, and store the result in dists[i, :]. #
# Do not use np.linalg.norm(). #
#######################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
delta = (self.X_train-X[i])**2
dists[i] = delta.sum(axis=1)
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
return dists
不让使用循环的写法推导稍微麻烦一些,主要是对 numpy 不是很熟悉,一些矩阵操作不知道怎么转化为对应的语句。大致思路是,将原式中的平方项完全展开,然后分别计算,最后相加。
def compute_distances_no_loops(self, X):
"""
Compute the distance between each test point in X and each training point
in self.X_train using no explicit loops.
Input / Output: Same as compute_distances_two_loops
"""
num_test = X.shape[0]
num_train = self.X_train.shape[0]
dists = np.zeros((num_test, num_train))
#########################################################################
# TODO: #
# Compute the l2 distance between all test points and all training #
# points without using any explicit loops, and store the result in #
# dists. #
# #
# You should implement this function using only basic array operations; #
# in particular you should not use functions from scipy, #
# nor use np.linalg.norm(). #
# #
# HINT: Try to formulate the l2 distance using matrix multiplication #
# and two broadcast sums. #
#########################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
x1 = (X**2).sum(axis=1)
x1 = x1.repeat(num_train).reshape(num_test, num_train)
x2 = (self.X_train**2).sum(axis=1)
x2 = x2.repeat(num_test).reshape(num_train, num_test)
x2 = x2.T
x3 = 2*np.dot(X,self.X_train.T)
dists = x1+x2-x3
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
return dists
后面就是快乐的验证环节了。在k=1时,获得了27.4\%的正确率,k=5时正确率略有提升,达到了27.8\%,和题面中的描述相符,基本上可以确定代码实现没有问题。
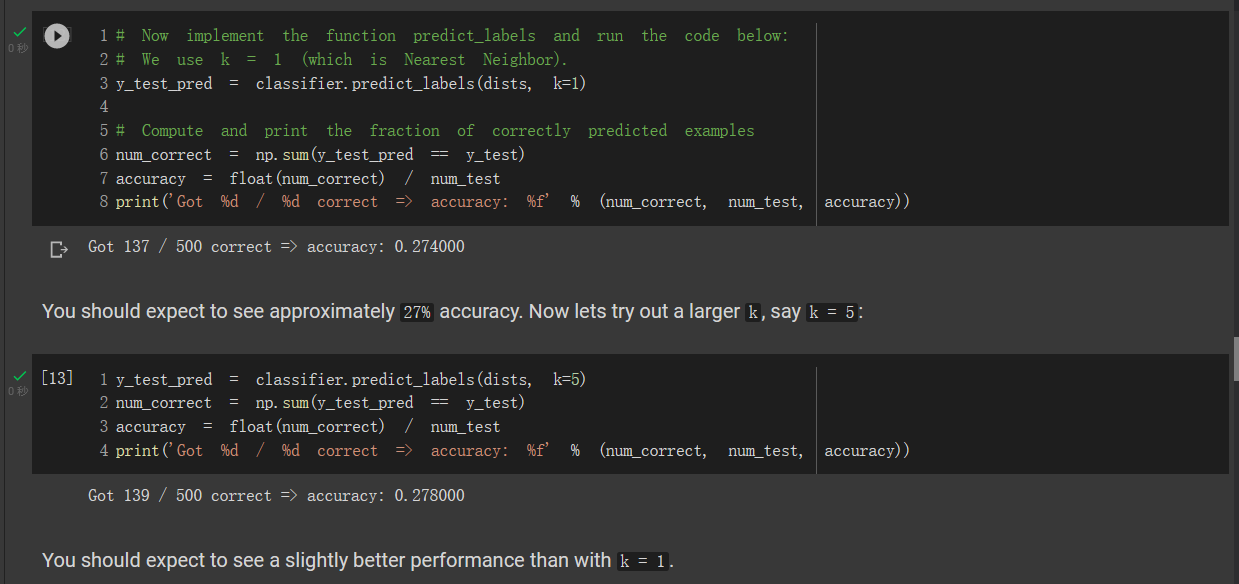
后面是对1重循环实现的检验。在检验时使用了 Frobenius 范数。所谓 Frobenius 范数,就是矩阵所有元素的平方和再开方。两个矩阵的范数几乎完全相同:
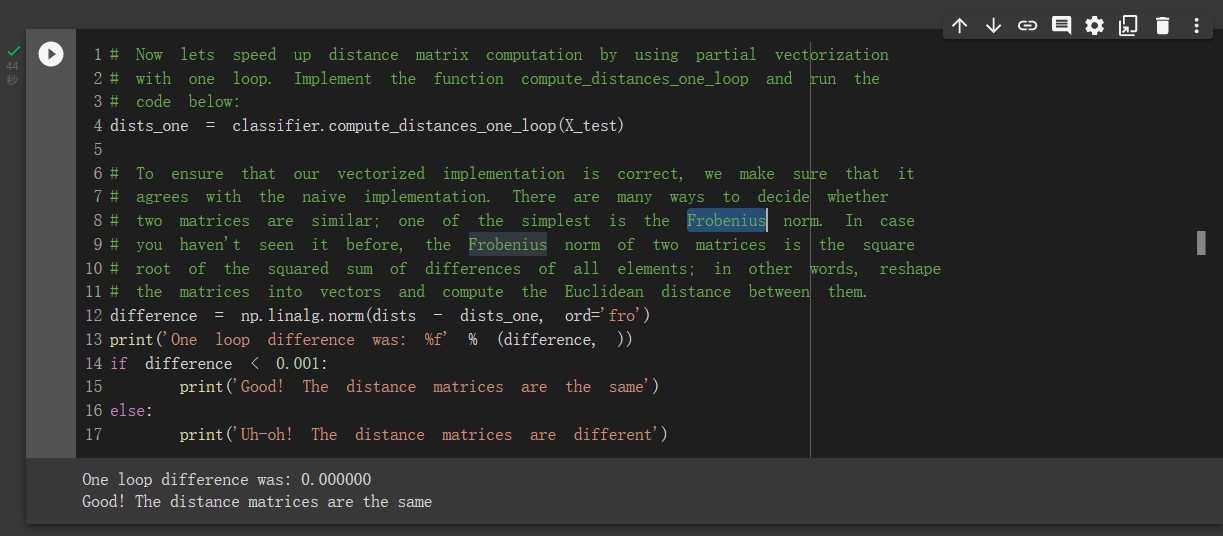
0重循环也是一样:
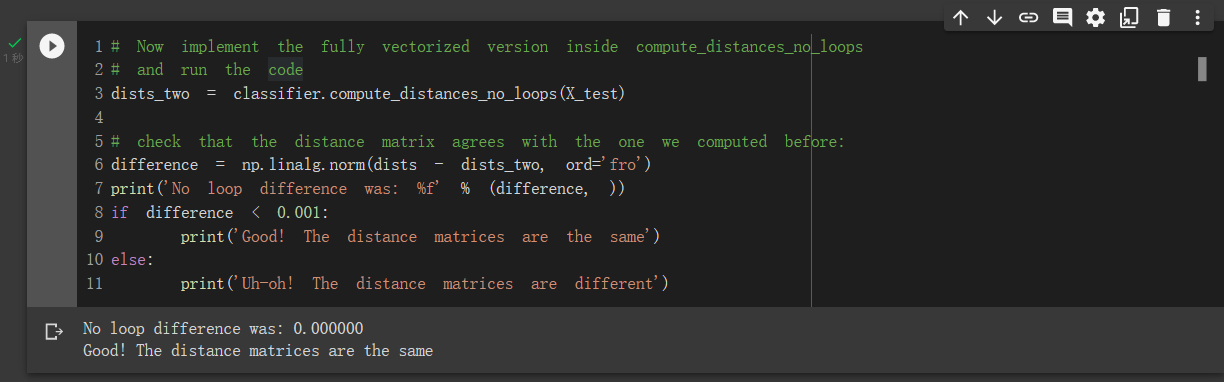
最后是三种实现的速度比较:
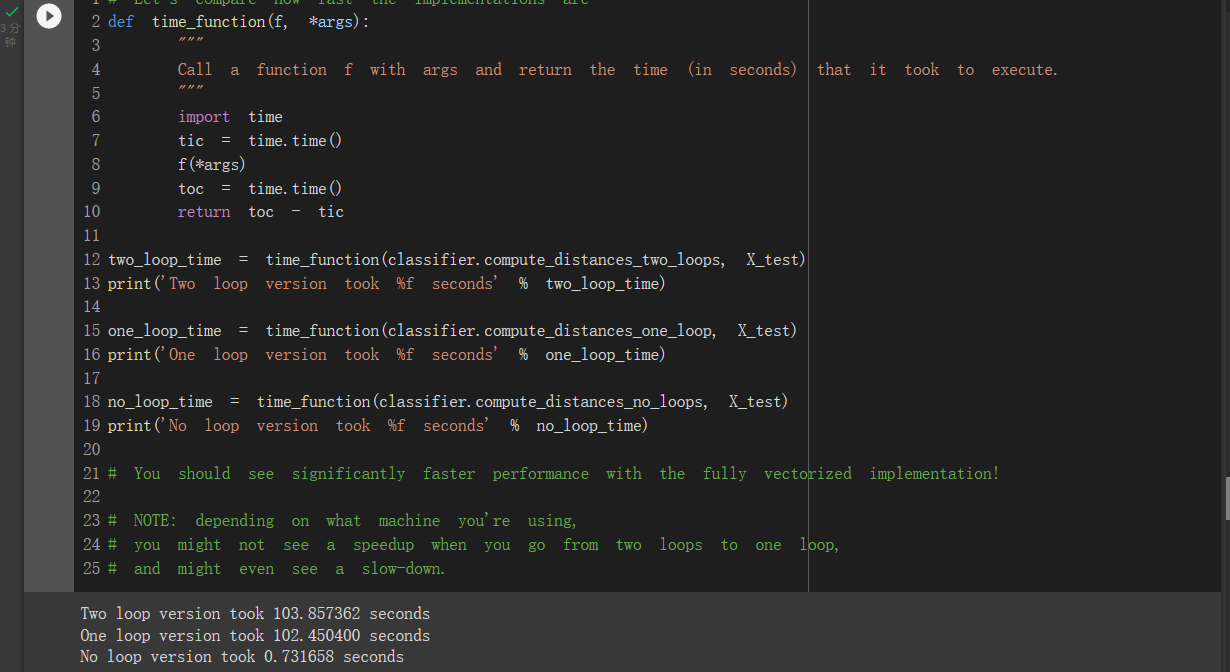
结果出来前卡了很久,完全没有想到纯向量计算可以省下这么多时间。
交叉验证
这一部分是实现对超参数k的交叉验证。任务是将训练集分为5个部分,每次选择其中的4个部分构成新的训练集,剩下的一个部分作为验证集,跑5次 KNN 检验k的效果。完整版代码如下:
num_folds = 5
k_choices = [1, 3, 5, 8, 10, 12, 15, 20, 50, 100]
X_train_folds = []
y_train_folds = []
################################################################################
# TODO: #
# Split up the training data into folds. After splitting, X_train_folds and #
# y_train_folds should each be lists of length num_folds, where #
# y_train_folds[i] is the label vector for the points in X_train_folds[i]. #
# Hint: Look up the numpy array_split function. #
################################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
length = X_train.shape[0] // num_folds
for i in range(num_folds):
X_train_folds.append(X_train[i*length:(i+1)*length,:])
y_train_folds.append(y_train[i*length:(i+1)*length])
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
# A dictionary holding the accuracies for different values of k that we find
# when running cross-validation. After running cross-validation,
# k_to_accuracies[k] should be a list of length num_folds giving the different
# accuracy values that we found when using that value of k.
k_to_accuracies = {}
################################################################################
# TODO: #
# Perform k-fold cross validation to find the best value of k. For each #
# possible value of k, run the k-nearest-neighbor algorithm num_folds times, #
# where in each case you use all but one of the folds as training data and the #
# last fold as a validation set. Store the accuracies for all fold and all #
# values of k in the k_to_accuracies dictionary. #
################################################################################
# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
for k in k_choices:
k_to_accuracies[k] = []
for i in range(num_folds):
test = np.array([])
labels = np.array([])
for j in range(num_folds):
if j!=i:
if test.shape[0] == 0:
test = X_train_folds[j]
labels = y_train_folds[j]
else:
test = np.vstack((test, X_train_folds[j]))
labels = np.vstack((labels, y_train_folds[j]))
labels = labels.reshape(4000)
classifier.train(test, labels)
dists = classifier.compute_distances_no_loops(X_train_folds[i])
print(k)
pred = classifier.predict_labels(dists, k=k)
num_correct = np.sum(pred == y_train_folds[i])
accuracy = float(num_correct) / (length * (num_folds-1))
k_to_accuracies[k].append(accuracy)
# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
# Print out the computed accuracies
for k in sorted(k_to_accuracies):
for accuracy in k_to_accuracies[k]:
print('k = %d, accuracy = %f' % (k, accuracy))
绘制出的交叉验证的结果如下图所示:
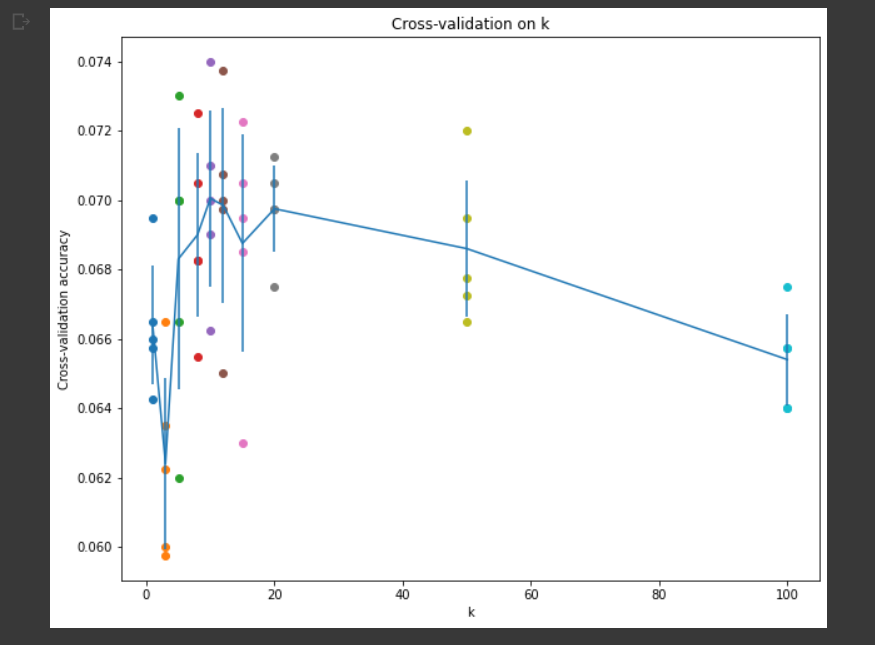
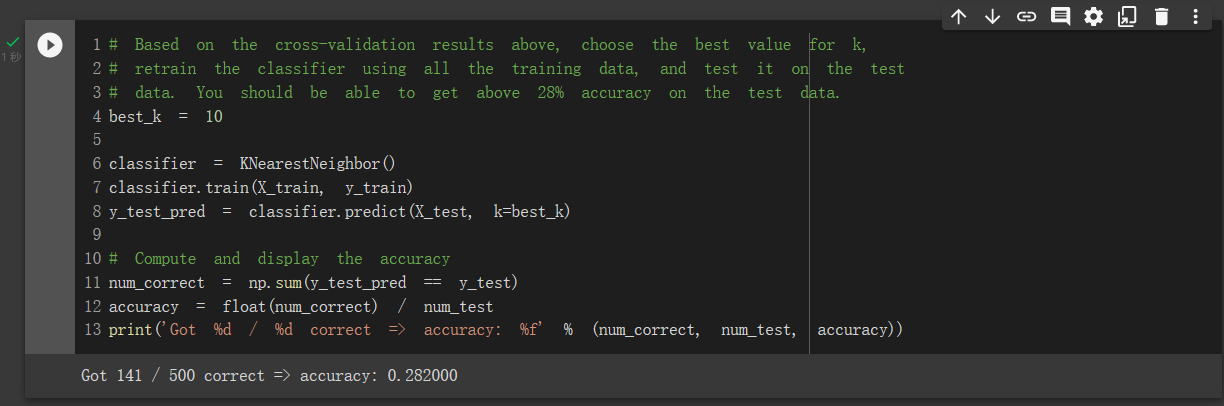
从图上可以看出 k 在取到10,13的时候最优。将 k=10 代入,最终在测试集上取得了28.2\%的正确率,符合描述。
Inline Question
KNN 部分有三道 Inline Question,相当于简答题。在这里给出我自己的答案(已参考过网上的答案)。
Q1
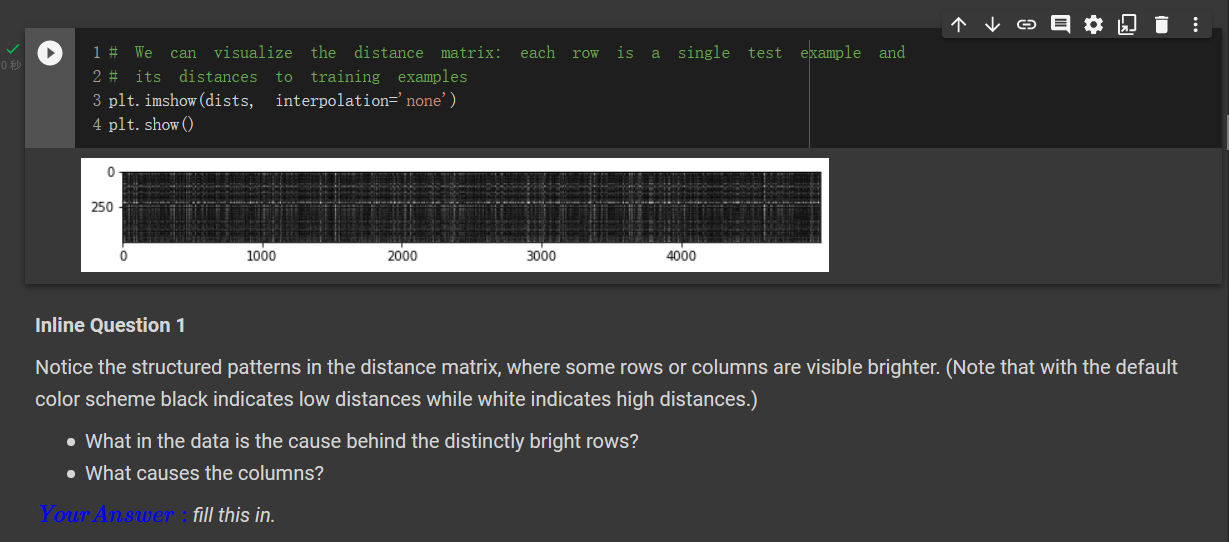
上面的图是距离矩阵。横坐标是测试集编号,纵坐标是训练集编号。图中白色的部分说明矩阵该位置的值较大,黑色说明值较小。
- Q : What in the data is the cause behind the distinctly bright rows?
- A : 测试集中有些图片长的很奇怪,和训练集中大部分图片都长的不太像。
- Q :What causes the columns?
- A :训练集中有一些图片,和测试集中大部分图片相似度都很低。
Q2

答案为1,3,5。
Q3

1错。考虑L2距离,平面上有一圈点围成一个圆,内部有另一个点,分属于两个类别。则边界会是一个环形,不是线性的。
2对。1-NN 只会找最接近的,也就是直接在训练集中找到了完全相同的图,而 5-NN 可能会有误差。
3错。测试集中随便构造一个数据集中没出现过的数据,就可以让 1-NN 分错,而 5-NN 能分类正确。
4对。从原理上不难得出。
感想
KNN 这一部分,代码实现的难度并不是很大,只在完成 no_loop 部分的时候由于对 numpy 不够熟悉卡了一会。毕竟是第一次作业,主要以熟悉 Python 与 Numpy 为主。
这种作业的形式个人非常喜欢,有很不错的正反馈,题目难度也适中,和视频搭配使用效果极佳,只能说不愧是斯坦福。
本文地址: 深度学习课程 CS231n Assignment1 KNN部分

